Correlated Gaussian Random Variables

 The function gnoise1 returns a nsample copies of m correlated random variables with mean = 0 and specified covariance matrix var. The algorithm uses the standard Cholesky decomposition (see section on Monte Carlo simulation at http://en.wikipedia.org/wiki/Cholesky_decomposition ). The matrix var must be symmetric and positive definite.

Function gnoise1(var,n)                                    // n draws of m-dim vector of corr. noise
    wave var; variable n                               // var must be sym, pos-def. matrix
    variable m=dimsize(var,0)
    MatrixOp /free cholesky=chol(var)                    // compute Cholesky decomposition
    make /d/free/n=(n,m) uncorr=gnoise(1)             // uncorrelated N(0,1) data
    MatrixOp /o corrdat = uncorr x cholesky
End


Here is a driver routine to demonstrate how it works (for 2d noise of specified correlation coefficient rho):

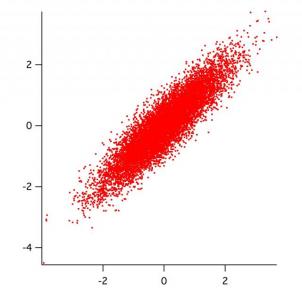
Function Demo2d(s1,s2,rho,nsamples,)   
    variable s1,s2,rho,nsamples                    // correlation coeff:  -1 < rho < 1
    make /d/o/n=(2,2) var={{s1^2, rho*s1*s2},{rho*s1*s2,s2^2}}     // make 2x2 covariance matrix
    gnoise1(var,nsamples);      wave corrdat

    Display corrdat[*][1] vs corrdat[*][0]
    ModifyGraph height={Plan,1,left,bottom}, mode=2, lSize=2
End


You can call it with
Demo2d(1,1,0.9,1e4)


and it should look like the attached graph.
Bech's code snippet can be used to visualise covariance matrices obtained from a Curvefitting algorithm, typically Funcfit.
It needs to be adapted a bit in this case, as the covariance matrix has NaN entries for the parameters that are being held. The following code snippet takes the fitted coefficients from Funcfit, along with the covariance matrix, and the holdstring (specifying which parameters are being held), and creates 2D wave called M_montecarlo.
This wave has howmany rows, and numpnts(coefs) columns.
Each of the rows contains a set of parameters which could be fed to the fit function used. Futhermore, for a given (parameter) column the mean and standard deviation of that column is equal to the fitted parameter and it's uncertainty. Moreover, different columns possess the correct covariance as specified by the input covariance matrix.


Function gen_synthMCfmCovar(coefs, M_covar, holdstring, howmany)
        //coefs from the curvefitting
        //M_covar from the curvefitting output
        //holdstring - the holdstring used for the fit.
        //how many samples you want to synthesize.

    wave coefs, m_covar
    string holdstring
    variable howmany

    variable varying = 0, ii, whichcol
    duplicate/free coefs, tempcoefs
    duplicate/free M_covar, tempM_covar

    varying = strlen(holdstring)
    for(ii = dimsize(coefs, 0)-1 ; ii >= 0 ; ii-=1)
        if(str2num(holdstring[ii]))
            deletepoints/M=0 ii, 1, tempcoefs, tempM_covar
            deletepoints/M=1 ii, 1, tempM_covar
            varying -=1
        endif
    endfor

    //create some gaussian noise
    make /free/d/n=(varying, howmany) noises = gnoise(1., 2)
    //and create the correlated noise from the covariance matrix.
    matrixop/free correlatedNoises = (chol(tempm_covar) x noises)^t

    make/n=(howmany, dimsize(coefs, 0))/d/o M_montecarlo
    Multithread M_montecarlo[][] = coefs[q]

    //now add the correlated noise back to the parameters
    whichcol = dimsize(correlatedNoises, 1) - 1
    for(ii = dimsize(coefs, 0)-1 ; ii >= 0 ; ii-=1)
        if(!str2num(holdstring[ii]))
            M_montecarlo[][ii] += correlatedNoises[p][whichCol]
            whichCol -= 1
        endif
    endfor

End

July 14, 2013 at 04:54 pm - Permalink

Very nice snippet!

I couldn't resist the temptation to try it in 3D. The new command line, demo function and Gizmo macro are:
•Demo3d(1,1,1,0.9,1e4)

Function Demo3d(s1,s2,s3,rho,nsamples,)
    variable s1,s2,s3,rho,nsamples                     // correlation coeff:  -1 < rho < 1
    make /d/o/n=(3,3) var2={{s1^2, rho*s1*s2, rho^2*s1*s3},{rho*s1*s2,s2^2, rho*s2*s3}, {rho^2*s1*s3,rho*s2*s3,s3^2}}      // make 3x3 covariance matrix
    gnoise1(var2,nsamples);
    wave corrdat
    Execute "Gizmo0()"
End

Window Gizmo0() : GizmoPlot
    PauseUpdate; Silent 1   // Building Gizmo 6 window...

    // Do nothing if the Gizmo XOP is not available.
    if(exists("NewGizmo")!=4)
        DoAlert 0, "Gizmo XOP must be installed"
        return
    endif

    NewGizmo/N=Gizmo0/T="Gizmo0"
    ModifyGizmo startRecMacro
    MoveWindow 17.25,53.75,317.25,289.25
    AppendToGizmo Scatter=root:corrdat,name=scatter0
    ModifyGizmo ModifyObject=scatter0 property={ scatterColorType,3}
    ModifyGizmo ModifyObject=scatter0 property={ markerType,0}
    ModifyGizmo ModifyObject=scatter0 property={ sizeType,0}
    ModifyGizmo ModifyObject=scatter0 property={ rotationType,0}
    ModifyGizmo ModifyObject=scatter0 property={ Shape,1}
    ModifyGizmo ModifyObject=scatter0 property={ size,1}
    ModifyGizmo ModifyObject=scatter0 property={ markerCTab,Rainbow}
    ModifyGizmo ModifyObject=scatter0 property={ CTABScaling,16}
    AppendToGizmo Axes=boxAxes,name=axes0
    ModifyGizmo ModifyObject=axes0,property={0,axisRange,-1,-1,-1,1,-1,-1}
    ModifyGizmo ModifyObject=axes0,property={1,axisRange,-1,-1,-1,-1,1,-1}
    ModifyGizmo ModifyObject=axes0,property={2,axisRange,-1,-1,-1,-1,-1,1}
    ModifyGizmo ModifyObject=axes0,property={3,axisRange,-1,1,-1,-1,1,1}
    ModifyGizmo ModifyObject=axes0,property={4,axisRange,1,1,-1,1,1,1}
    ModifyGizmo ModifyObject=axes0,property={5,axisRange,1,-1,-1,1,-1,1}
    ModifyGizmo ModifyObject=axes0,property={6,axisRange,-1,-1,1,-1,1,1}
    ModifyGizmo ModifyObject=axes0,property={7,axisRange,1,-1,1,1,1,1}
    ModifyGizmo ModifyObject=axes0,property={8,axisRange,1,-1,-1,1,1,-1}
    ModifyGizmo ModifyObject=axes0,property={9,axisRange,-1,1,-1,1,1,-1}
    ModifyGizmo ModifyObject=axes0,property={10,axisRange,-1,1,1,1,1,1}
    ModifyGizmo ModifyObject=axes0,property={11,axisRange,-1,-1,1,1,-1,1}
    ModifyGizmo ModifyObject=axes0,property={-1,axisScalingMode,1}
    ModifyGizmo ModifyObject=axes0,property={-1,axisColor,0,0,0,1}
    ModifyGizmo modifyObject=axes0 property={Clipped,0}
    AppendToGizmo freeAxesCue={0,0,0,1},name=freeAxesCue0
    ModifyGizmo setDisplayList=0, opName=ortho0, operation=ortho, data={-2.5,2.5,-2,2,-2,2}
    ModifyGizmo setDisplayList=1, object=freeAxesCue0
    ModifyGizmo setDisplayList=2, object=scatter0
    ModifyGizmo setDisplayList=3, object=axes0
    ModifyGizmo SETQUATERNION={-0.197844,0.141310,0.028073,0.969590}
    ModifyGizmo autoscaling=1
    ModifyGizmo currentGroupObject=""
    ModifyGizmo compile

    ModifyGizmo userString={wmgizmo_df,"Gizmo0"}
    ModifyGizmo endRecMacro
End

The Gizmo plot should resemble the attached figure. (The Gizmo Macro and figure have been updated to include a display enhancement suggested by WaveMetrics' AG.)
Gizmo0ExportedNew.pdf (15.28 KB)

July 17, 2013 at 03:24 am - Permalink

Forum

Support

Gallery

Igor Pro 9

Learn More

Igor XOP Toolkit

Learn More

Igor NIDAQ Tools MX

Learn More