The Jarque-Bera demo experiment can be used to generate the null distribution of the Jarque-Bera statistic for any number of variables (N). The Jarque-Bera statistic has asymptotically the Chi-square distribution with two degrees of freedom, i.e., StatsChiCDF(x,2). For small value of N the actual distribution is sufficiently different from the asymptotic values.

The calculation consists of a Monte-Carlo simulation which computes the Jarque-Bera statistic for many realizations of N random samples from a normal distribution. The wave containing the statistic is histogramed (using the /P flag it is also normalized as a PDF) and then integrated to get the corresponding CDF.

To obtain the critical value you can solve for the point at which the CDF equals 1-alpha, where alpha is the desired significance.

To run the simulation execute the following command.

This will run 1 million iterations for N=22. The resulting CDF is stored in the wave W_JBCDF shown below.

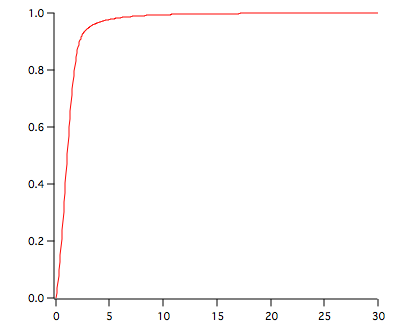
To find the critical value for alpha=0.05 execute the command:

The results are: V_LevelX= 3.09913; V_rising= 1;

By comparison, the asymptotic approximation is give by:

which yields 5.99146.

This indicates that for N=22 there is a significant difference between the asymptotic approximation and the critical value obtained from this calculation.

More Details

The simulation uses WaveStats to compute skewness and kurtosis. WaveStats uses a two-pass algorithm to compute the higher order moments (i.e., the first pass computes the average value and the second pass computes the various central moments). The two-pass algorithm is supposed to provide higher accuracy (see, for example, a discussion in Numerical Recipes) then algorithms that evaluate the binomial expansion sums of wave elements. Here is an example of the difference between the two methods of computation:

Kurtosis(WaveStats)=-0.013552

Kurtosis(binomial expansion sums)=-0.0134328