When you fit a model to data, it is usually assumed that all errors are in the dependent variable, and that independent variables are known perfectly (that is, X is set perfectly and Y is measured with error). This assumption is often not far from true, and as long as the errors in the dependent variable are much larger than those for the independent variable, it will not usually cause much difference to the curve fit.

When the errors are normally distributed with zero mean and constant variance, and the model is exact, then the standard least-squares fit gives the maximum-likelihood solution.

In some cases, however, the errors in both dependent and independent variables may be comparable. This situation has a variety of names including errors in variables, measurement error models or random regressor models. An example of a model that can result in similar errors in dependent and independent variables is fitting the track of an object along a surface; the variables involved would be measurements of cartesian coordinates of the object's location at various instants in time. Presumably the measurement errors would be similar because both involve spatial measurement.

Fitting such data using standard or ordinary least squares can lead to bias in the solution. To solve this problem, we offer Orthogonal Distance Regression (ODR). Rather than minimizing the sum of squared errors in the dependent variable, ODR minimizes the orthogonal distance from the data to the fitted curve by adjusting both the model coefficients and an adjustment to the values of the independent variable. This is also sometimes called "total least squares".

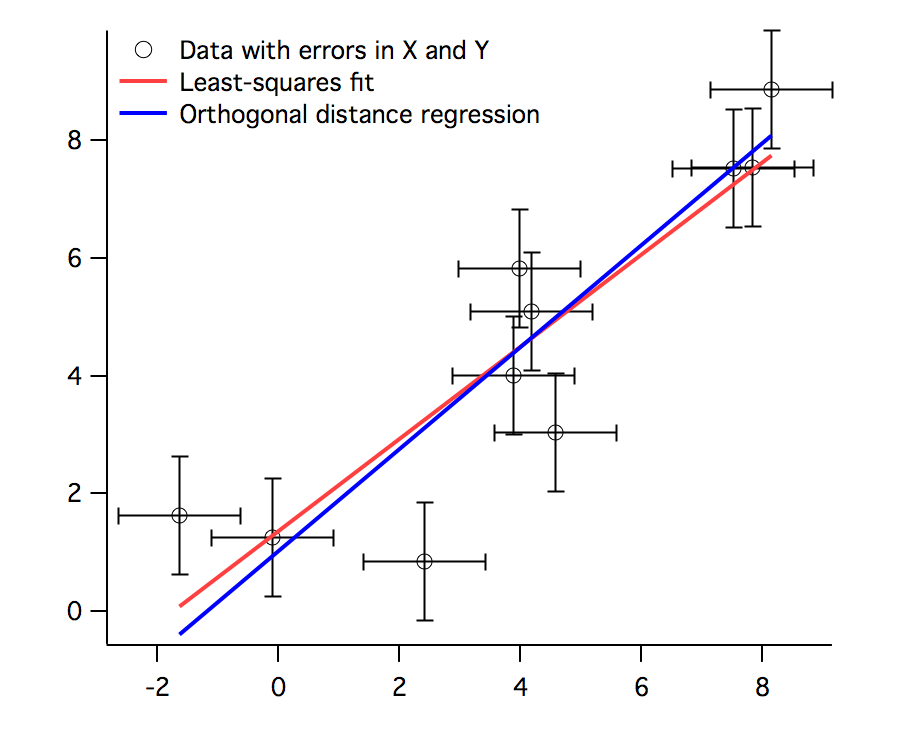
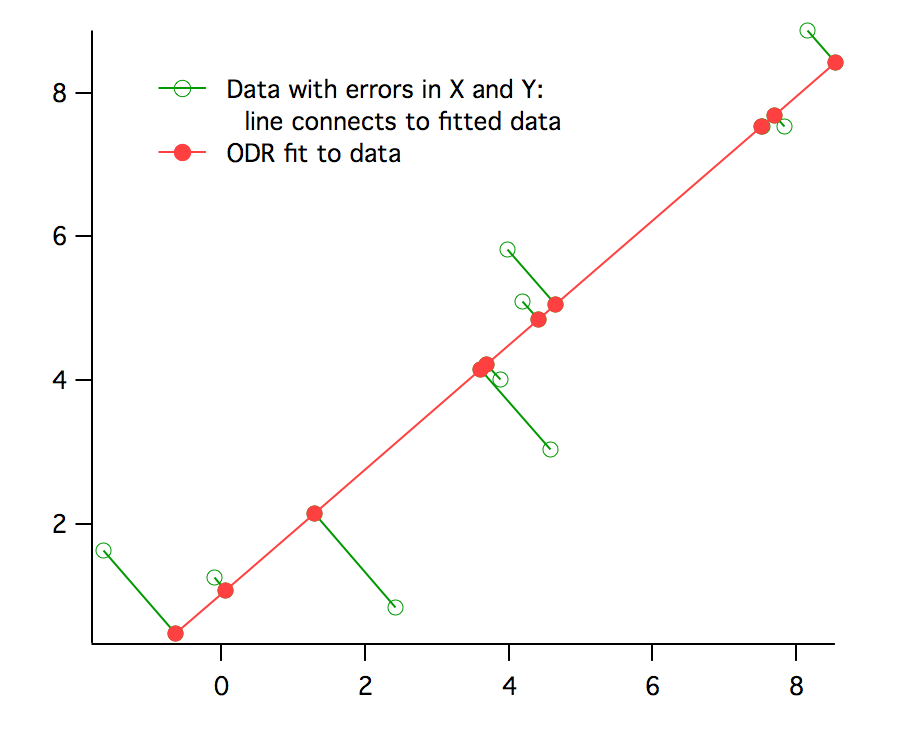
For ODR curve fitting, Igor Pro® uses the freely available ODRPACK95. For more information, consult these papers:

Boggs, P.T., R.H. Byrd, and R.B. Schnabel, A Stable and Efficient Algorithm for Nonlinear Orthogonal Distance Regression, SIAM Journal of Scientific and Statistical Computing, 8, 1052-1078, 1987.

Boggs, P.T., R.H. Byrd, J.R. Donaldson, and R.B. Schnabel, Algorithm 676 - ODRPACK: Software for Weighted Orthogonal Distance Regression, ACM Transactions on Mathematical Software, 15, 348-364, 1989

Boggs, P.T., J.R. Donaldson, R.B. Schnabel and C.H. Spiegelman, A Computational Examination of Orthogonal Distance Regression, Journal of Econometrics, 38, 169-201, 1988.