FFT of even-symmetric function yields non-negligible imaginary part

Share icon

I performed FFT on a cosine function with even symmetricity around zero. Based on the Fourier transform principle, I did not expect any imaginary part in the transformed profile. However, the imaginary part always exists. Do you have any suggestions about what is wrong with my code?

function corr()
   
    variable xmin = -1
    variable xmax = 1
   
    make/N=21/O tt
   
    SetScale/I x, xmin, xmax, tt
    tt = cos(2*pi*x)
    deletePoints 20, 1, tt // delete last point
   
    FFT/OUT=1/PAD={100000}/DEST=tt_FFT  tt

end

 

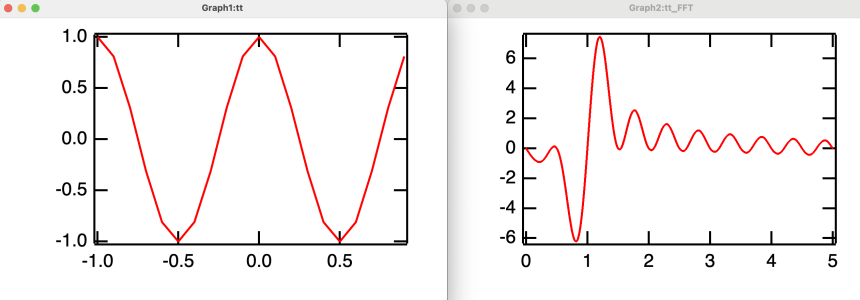
 FFT of cosine function

I believe your mistake is to pad using the FFT. You would be better to wrap the function. See the illustration. You have to wrap manually.

Try the function below with variations to npnts and with nopad present or not.

function calc_corr(variable npnts, [variable nopad])
   
    variable xmin = -1
    variable xmax = 1
   
    make/N=(npnts)/O tt
   
    SetScale/I x, xmin, xmax, tt
    tt = cos(2*pi*x)
    deletePoints 20, 1, tt // delete last point
    if(ParamIsDefault(nopad))
        FFT/OUT=1/PAD={100000}/DEST=tt_FFT  tt
    else
        FFT/OUT=1/DEST=tt_FFT  tt
    endif
    return 0
end

 
pad versus wrap (154.68 KB)

January 18, 2025 at 03:22 pm - Permalink