Rearranging a 2D point set to enclose the set with a line
sjr51
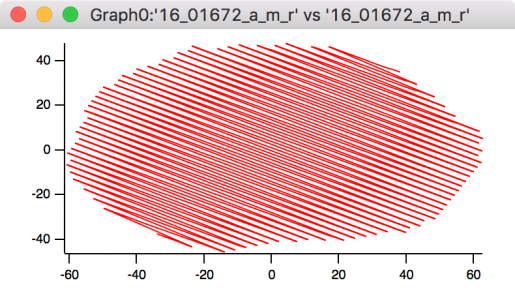
I am out of ideas and would appreciate any help. I have several sets of xy coords that form an approximately elliptical border (they are locations of a segmented region of an image). When I pulled them from the image they were arranged in a vertically ascending order. I'd like to rearrange them into a clockwise (or anti-clockwise) order so that the points form a border around the ellipse, like in the original image. Does anyone have an idea how to do this? I am attaching a picture of the plot as it stands. Essentially, I want to get rid of the zig-zag pattern.
Unfortunately, the order is not alternating (it looks like it from the image) so re-arranging it that way doesn't work. I've tried that!
Find the center (average x and y) and then calculate the angle from the center to the point and then sort the wave based on the angle.
Andy
June 27, 2017 at 08:02 am - Permalink
June 27, 2017 at 08:16 am - Permalink
I think you will also have to make your own ellipse 'x' and 'y' waves from the best-fit parameters, because the automatically created waves will follow the original sorting irregularity.
June 27, 2017 at 08:40 am - Permalink
Have you tried ConvexHull?
June 27, 2017 at 10:32 am - Permalink
It seems to me that ConvexHull might miss some end points that are close to the boundary, but slightly concave. Your help file example show at least one point illustrating such behavior. Stephen's data show other such potential problem points. Perhaps that is not an issue for him.
June 27, 2017 at 10:54 am - Permalink
best,
_sk
June 27, 2017 at 11:49 am - Permalink
If any point goes missing, one can use the convex hull path and solve for the shortest distance from the missing points to the hull path. The intersection with the hull-path would determine the order of the point in the sequence.
June 27, 2017 at 12:22 pm - Permalink
I have another idea. It may not be too elegant but gave me the possibility to test my understanding of conditional operators. It expects the non-ordered coordinates in two waves and gives the ordered coordinates in two new waves (x_oval and y_oval).
I have tested it only with one hand-drawn example. It could give problems when two or more points lie exactly on a horizontal or vertical line.
I hope it helps.
Greetings, Klaus
#pragma rtGlobals=3 // Use modern global access method and strict wave access.
function oval(xp, yp)
wave xp, yp
variable x1, y1, x2, y2, x3, y3, x4, y4
wavestats/q xp
x1 = v_min
y1= yp[V_minloc]
x3 = V_max
y3 = yp[V_maxloc]
wavestats/q yp
x2 = xp[V_maxloc]
y2 = v_max
x4 = xp[V_minloc]
y4 = V_min
duplicate /o xp x1p, x2p, x3p, x4p
duplicate /o yp y1p, y2p, y3p, y4p
x1p = (x1 <= xp[p] && xp[p] < x2) && (y1 <= yp[p] && yp[p] < y2) ? xp[p] : NaN
y1p = (x1 <= xp[p] && xp[p] < x2) && (y1 <= yp[p] && yp[p] < y2) ? yp[p] : NaN
WaveTransform zapnans x1p
WaveTransform zapnans y1p
sort x1p, x1p, y1p
x2p = (x2 <= xp[p] && xp[p] < x3) && (y2 >= yp[p] && yp[p] > y3) ? xp[p] : NaN
y2p = (x2 <= xp[p] && xp[p] < x3) && (y2 >= yp[p] && yp[p] > y3) ? yp[p] : NaN
WaveTransform zapnans x2p
WaveTransform zapnans y2p
sort x2p, x2p, y2p
x3p = (x3 >= xp[p] && xp[p] > x4) && (y3 >= yp[p] && yp[p] > y4) ? xp[p] : NaN
y3p = (x3 >= xp[p] && xp[p] > x4) && (y3 >= yp[p] && yp[p] > y4) ? yp[p] : NaN
WaveTransform zapnans x3p
WaveTransform zapnans y3p
sort /r x3p, x3p, y3p
x4p = (x4 >= xp[p] && xp[p] > x1) && (y4 <= yp[p] && yp[p] < y1) ? xp[p] : NaN
y4p = (x4 >= xp[p] && xp[p] > x1) && (y4 <= yp[p] && yp[p] < y1) ? yp[p] : NaN
WaveTransform zapnans x4p
WaveTransform zapnans y4p
sort /r x4p, x4p, y4p
Concatenate /O /NP /KILL {x1p,x2p,x3p,x4p}, x_oval
Concatenate /O /NP /KILL {y1p,y2p,y3p,y4p}, y_oval
end
June 27, 2017 at 01:12 pm - Permalink
Yes. Here is one 2D wave, column 0 is x and column 1 is y.
June 27, 2017 at 11:22 pm - Permalink
Thank you. Yes, I have already been down this path. Actually these final point sets have been centred at the origin and rotated so that the semimajor axis along x at y=0 and semiminor is along y at x=0 so the fit is similar to the example in the manual. The problem is that I want the plots to look like the real data and not a fit to it.
June 27, 2017 at 11:26 pm - Permalink
Thank you for the suggestion. Yes, I'd like all points recovered and this put me off convex hull. I like this idea of recovering the other points and hadn't thought of that as a solution when fitting a convex hull for other problems - I had investigated "alpha shapes" as a solution and not got very far with that.
June 27, 2017 at 11:31 pm - Permalink
Hi Klaus,
Thank you for your answer and your code! I just tried one point set. It **nearly** worked for my data (see attached pic). From the original image I do have several consecutive horizontal and vertical values because they are pixel locations. However, because of the rotation I thought that these values would no longer be horizontal or vertical, so it should work. I'll investigate a bit more. Thank you.
June 27, 2017 at 11:40 pm - Permalink
Andy's idea worked and my code is below in case it is useful for anyone. Note that the points are centred at the origin and atan2 is used to get unique values for theta round one rotation.
I pass the 2-column wave to this as part of a larger stack.
Function Threader(m1)
Wave m1
String mName = NameOfWave(m1)
MatrixOp/O c0 = col(m1,0)
MatrixOp/O c1 = col(m1,1)
Variable nRows = DimSize(m1,0)
Make/O/FREE/N=(nRows) threadW=0
// measure angles, store in threadW
Variable theta
Variable i
for(i = 0; i < nRows; i += 1)
theta = atan2(c1[i],c0[i])
threadW[i] = theta
endfor
// sort x coords and ycoords based on theta
Sort threadW, c0, c1
// add last point equal to first to complete the shape
InsertPoints nRows,1, c0,c1
c0[nRows] = c0[0]
c1[nRows] = c1[0]
// put back together and overwrite original
Concatenate/O/KILL {c0,c1}, $mName
End
June 28, 2017 at 12:35 am - Permalink