Fit functions using convolution - how to elegantly fit sections of a curve

Share icon

I've got this rather complicated function to fit experimental data from a photon counting experiment. To take into account the time-resolution of the detector, my fit function performs a convolution with the instrument response function. I think this is pretty common way to deal with this kind of data and so far it has worked well for me (i.e. the blue curve in the attached plot fits my data reasonable well).

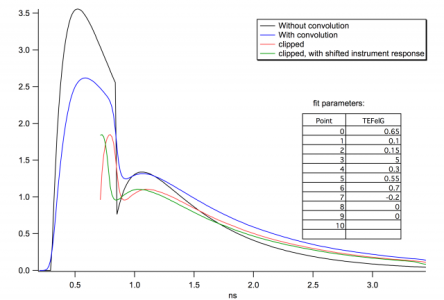
The problem starts when I want to fit a small section of the curve - the outcome is the red curve in the plot. There is clearly an issue with the convolution on the left side of the curve. I've found I can improve the curve by shifting the instrument response (green curve), but there is still an artefact, and now the right side of the curve is affected as well.

Here is my code:

Function twoExpFelConvTest(pw, yw, xw) : FitFunc
    WAVE pw, yw, xw
   
    xw = xw - pw[4]
    Variable a = exp(-(pw[5]/pw[1]))
    Variable b = ((exp(-(pw[5]/pw[0])) - exp(-(pw[5]/pw[1])))*pw[0])/(pw[0] - pw[1])
    yw = pw[3]*(xw>=0) * ( (xw<pw[5])*(((exp(-(xw/pw[0])) - exp(-(xw/pw[1])))*pw[0])/(pw[0] - pw[1])) + (xw>=pw[5])*((exp(xw/pw[0])*pw[0]*(b*exp(xw/pw[1] + pw[5]/pw[2])*(pw[7] + pw[6])*(-pw[0] + pw[1]) + a*exp(xw/pw[2] + pw[5]/pw[1])*(-pw[0] + pw[2])) + exp(xw*(1/pw[1] + 1/pw[2]) + pw[5]/pw[0])*(a*pw[0]*(pw[0] - pw[2]) + b*(pw[0] - pw[1])*((1 + pw[7])*pw[0] + (-1 + pw[6])*pw[2])))/exp(xw*(1/pw[0] + 1/pw[1] + 1/pw[2]))/((pw[0] - pw[1])*(pw[0] - pw[2])))  )
   
    Convolve/A root:convolvedFitting:laserResponseL2, yw
    xw = xw + pw[4]
End


I've also attached a simple Igor experiment that demonstrates the problem.

I was wondering if anyone has encountered this problem before. I believe the standard way to deal with this would be to add data points to either side of the curve with linear regression, and remove them again after convolution. However, this doesn't seem very elegant, since I already know how the curve will continue on either side (I just don't want to include these data points in the fit). Another idea that I had was to fit the entire curve in the Curve fit dialog, but then use two extra fit parameters to define the range I really want. I'm not sure though how Igor will react when my fit function return less data points than it was given.

Does anyone have some useful suggestions? clipped and convolved transients.pxp (117.01 KB)
I think you need to compute the entire kernel, do the convolution, and then extract the points corresponding to the X values in xw. That will involve creating a temporary wave for the full model, and then assigning to yw at the very end. Right now, if you try to fit to a subrange of your data, you are convolving a truncated bit of the kernel, and you will get those edge effects from the ends where the impulse response laps off the ends of your model. You need to make sure the kernel either extends beyond the region of interest by at least the number of points in your impulse response, or extends far enough that the kernel goes to zero.
Function twoExpFelConvTest(pw, yw, xw) : FitFunc
    WAVE pw, yw, xw
 
    Make/D/FREE/N=(compute reasonable number of points) tempyw
    SetScale/I x (compute min X value required), (compute max X value required), tempyw
    // From here, use the scaled X value instead of xw
    Variable a = exp(-(pw[5]/pw[1]))
    Variable b = ((exp(-(pw[5]/pw[0])) - exp(-(pw[5]/pw[1])))*pw[0])/(pw[0] - pw[1])
    tempyw = pw[3]*(x>=0) * ( (x<pw[5])*(((exp(-(x/pw[0])) ...
 
    Convolve/A root:convolvedFitting:laserResponseL2, tempyw
    // Now extract just the values you need from the entire computed model
    yw = tempyw(xw[p])      // you need to figure out exactly what goes here
End



John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

June 22, 2015 at 03:04 pm - Permalink

Thank you John, your idea worked great! In case anyone else stumbles across the same problem, here is the code I ended up using:

Function twoExpFelConvTest2(pw, yw, xw) : FitFunc
    WAVE pw, yw, xw

    Variable size = numpnts(yw)
    Variable padding = 248
    Make/FREE/D/N=(size+2*padding) tempyw
    Variable delta = (xw[numpnts(xw)-1] - xw[0]) / (numpnts(xw)-1);
    SetScale/I x xw[0]-padding*delta, xw[numpnts(xw)-1]+padding*delta, tempyw
    Variable a = exp(-(pw[5]/pw[1]))
    Variable b = ((exp(-(pw[5]/pw[0])) - exp(-(pw[5]/pw[1])))*pw[0])/(pw[0] - pw[1])
    tempyw = pw[3]*(x>=0) * ( (x<pw[5])*(((exp(-(x/pw[0])) - ...

    Convolve/A root:convolvedFitting:laserResponseR, tempyw
   
    yw = tempyw(xw[p])
End

June 23, 2015 at 07:04 am - Permalink

I've just noticed another problem when using my fit function with the Curve Fitting dialog. It is important that the xw wave has got the same step size as the measured instrument response function, otherwise the time axis gets messed up during convolution. During the actual fitting process it works out, because I'm fitting curves that have been measured with the same parameters as the instrument response. However, the problem lies in the graphing before and after the fitting (i.e. when roughing in the parameters and plotting the results). Here, Igor always uses a fixed number of points, independent of the data you want to fit (the preset is 200 I think). Is there an easy method to make Igor use the same number of points for plotting as for fitting? I.e. when I'm fitting a section that has 50 points, I want Igor to use 50 points to plot the result. I realize I could set the number by hand in the Curve Fitting dialog, but this would be a pain, since I want to be able to fit sections of my curves which would have a different number of points every time. The other possibility would be to start with a large amount of points and do some sort of downsampling before convoluting, but this sounds so complicated I would only consider it as a last resort.

June 26, 2015 at 08:10 am - Permalink

Use the /D= version of the /D flag. That uses a wave the same size as the input data, and is filled directly from the model computed for the fit, not from a separate evaluation.

It is possible, but a bit trickier to make your fit function independent of the number of points and X spacing. You just (?) need to compute the model at sufficiently high resolution, then extract the needed points using the xw wave to find the right model values. In fact, I think the fit function you wrote after my last post is almost there. You just need to remove the dependence on numpnts(xw) or numpnts(yw), and instead use some measure of needed resolution that you can compute.

In fact, upon re-reading your description of your problem, it's probably best just to use /D=. Note that needs to have as many points as the *entire* Y wave, not the 50-point subset. Igor will fill in just the points corresponding to the subset that you actually fit. Your fitting function won't be called separately to compute those points.

John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

June 26, 2015 at 01:57 pm - Permalink

John, thanks for your reply. I don't quite understand how to call FuncFit with the /D= flag (the manual is not as rigorous as it could be), could you please provide an example of the command?

Also: is there any chance this will work from the Curve Fitting Dialog? It would make my workflow much easier, since I need to adjust my initial fit parameters to my data before I start the actual fitting.

July 1, 2015 at 05:14 pm - Permalink

The help is rigorous, just hard to understand :)

The confusion, no doubt, is that there are two sets of flags, those at the beginning (right after the FuncFit keyword) and those at the end (after the Ywave). The /D flag you need is the one in the second set of flags.
Duplicate ywave, fitywave
FuncFit/someflags twoExpFelConvTest, w_coef, ywave /X=xwave/D=fitywave ...

The /D= option is available in the Curve Fit dialog on the Output Options tab. Choose _New Wave_ as the destination, enter a nice name in the edit box, and the commands to make and use that wave will be generated for you.
Quote:
I need to adjust my initial fit parameters to my data before I start the actual fitting.

Hmmm... I think perhaps the Graph Now button uses the auto-destination wave even if you choose to use an explicit destination via the Destination menu. You can explore it yourself, though. Here are commands that will do it, first if you have a waveform (just one wave with X values set by the wave's X scaling):
Duplicate ywave, fitywave
Duplicate ywave, fitxwave
fitxwave = x
Display fitywave
twoExpFelConvTest(coefs, fitywave, fitxwave)

You need a suitable coefficient wave, and substitute the real name of that wave for "coefs". I used "ywave" to stand in for your real Y data wave.

Now if you have an XY pair of waves:
Duplicate ywave, fitywave
Display fitywave vs xwave
twoExpFelConvTest(coefs, fitywave, xwave)

Here, I have used "xwave" to stand in for your real X data wave.
In either case, edit "coefs" to try new values, and re-execute the last line to see new results.

John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

July 2, 2015 at 11:30 am - Permalink

Thanks again for your suggestions, John. I've played around a little bit with the commands you provided. The /D= option works fine when I'm fitting the entire x-range, except that the output is not plotted when I'm working from the curve fitting dialog. However, when I fit a subrange, the output consists of the fit in this subrange, plus the original data at the edges - not quite what I expected. In addition, everything that's plotted from the curve fitting dialog seems to contain exactly 200 points or whatever is specified in the output options tab. In the end, I've decided that I'm going to set the number of points I need in the curve fitting dialog for every fit. It's not really my idea of elegant, but it seems to be the simplest solution.

Here's a suggestion for the next release: there should be an option in the output options tab of the curve fitting dialog that says "match output to input length" or something similar - it seems logical to me that you'd want an output point for every input point (not just for stuff involving convolutions), instead of getting an arbitrary amount of points - except of course when there's only a handful of input points.

July 7, 2015 at 08:38 am - Permalink

The auto-destination wave is intended to provide a smooth curve through your data, even if you have a small number of data points, a huge number of data points, or points that have wildly variable X spacing.

Your complaint about the /D= option leaving data in the unused parts of the wave can be "fixed" by pre-filling the wave with some value. NaN will result in blanks on the graph where you haven't fit the data. My example commands should be expanded like this:
Duplicate ywave, fitywave
fitywave = NaN              // or some value of your choosing
FuncFit/someflags twoExpFelConvTest, w_coef, ywave /X=xwave/D=fitywave ...

Quote:
In the end, I've decided that I'm going to set the number of points I need in the curve fitting dialog for every fit.

That will work if your data points are equally spaced in X. If they are not, some of the fit curve points will be in the wrong places.

John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

July 8, 2015 at 09:22 am - Permalink