Numerical precision - dawson(x) vs erfcw(real(x+iy))

Share icon

I am fitting spectroscopy transmission data of molecular gas absorption data with voigt lineshapes; we measure both phase and magnitude of the absorption lines.

For the phase fit, I use the complex error function erfcw when both a doppler (pressure) and lorentzian (collision) component is present, and the Dawson integral when only a doppler component is expected.

I noticed that I don't get the same phase using erfcw or dawson for doppler-only lineshapes. Ideally (i.e. analytically),
dawson(x)*2/sqrt(pi) = imag(erfcw(cmplx(x,0))

I noticed that this relationship is only true for |x|<~5; this is shown in the attached graph created with the macro at the bottom. Can anyone tell me which calculation is more accurate for large x?

thanks,
Fabrizio

macro testIt()<br />
    make/d/o/n=1000 Wdaw, Werf, delta; setscale/I x -50,50, Wdaw, Werf, delta<br />
    Wdaw=2/sqrt(pi)*dawson(x)<br />
    werf=imag(erfcw(cmplx(x,0)))<br />
    delta=abs((wdaw-werf)/werf)<br />
    display delta; ModifyGraph log(left)=1<br />
endmacro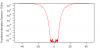
Hello Fabrizio,

Your macro uses the function erfcw() which is not in my version of IP (obviously my home copy needs an update).

The Dawson integral is computed from a series approximation. The erfc is usually computed from the Hyper-Geometric function which is, in general, a very messy series calculation. In other words both of these are not simple. IIRC the Dawson expression is going to be more accurate closer to zero. For large arguments I still expect the Dawson integral to be more accurate. There is a brief discussion of Dawson's accuracy in the reference provided in the IGOR help file.

If I had to guess (and if accuracy at large x really mattered to me) I'd use Dawson because it is a simpler and more straightforward calculation. If the built-in Dawson function does not provide sufficient accuracy one can look into using better expansions. Feel free to send details of your application and requirements to support@wavemetrics.com if you want us to help.

A.G.
WaveMetrics, Inc.

June 27, 2011 at 11:14 am - Permalink

Hello Fabrizio,

After a bit more investigation here are some details:

The Dawson integral is evaluated from a series of 24 terms. When x is large (x>20) you are going to see some degradation in accuracy simply because the integrand becomes unstable numerically. Erfcw is said to have accuracy to about 14 digits. The primary expansion in this approach is relatively more stable for large x.

If accuracy is really important you can have a bit more control (at the cost of computation time) using the error function. Note that the Dawson integral can also be evaluated using

Function/c FF(zz)
Variable/C zz

return -cmplx(0,(sqrt(pi)/2))*exp(-zz*zz)*erf(cmplx(0,1)*zz)
End

The advantage here is that erf() in the last expression can take an accuracy parameter. A word of caution though is that for large arguments and decent accuracy the hypergeometric function 1F1() used to compute the erf() can take a long time to converge.

HTH,

A.G.
WaveMetrics, Inc.

June 27, 2011 at 12:04 pm - Permalink

Thanks for your answers.

I just had a chance to compare with matlab. In Matlab, I used the built-in Dawson function and implemented the complex error function (aka Faddeeva function) according to J. A. C Weideman, 'Computation of the Complex Error Function', SIAM Journal on Numerical Analysis, Vol. 31, No 5 (Oct. 1994), pp. 1497-1518, using 30 terms.

The Matlab dawson agrees very well with the Igor erfcw, and the Weideman complex error function in Matlab is still doing fairly well, however the Igor Dawson stands apart... (see attached figure). More specifically, the igor Dawson function converges faster (I assume too fast...) towards zero for |x|>5.

I use Igor 6.2.2.2 on windows XP; the erfcw function seems to be part of Igor and is also described in the online and pdf help ... ?
DawsonMatlabIgor.png (56.29 KB)

June 28, 2011 at 12:35 pm - Permalink

This is a pretty old thread, but, for what it's worth, Igor 8 will feature a Dawson integral implementation with greatly improved accuracy outside the -5,5 range of inputs, and Dawson will accept complex inputs as well.

John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

October 27, 2016 at 12:25 pm - Permalink