
noise peak pickup in igor

syc33
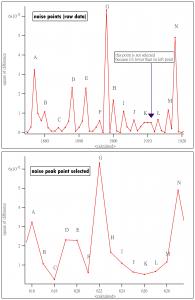
I am dealing with noise data on the strain curve against time from inverted force torsion pendulum. As the attached image, the noise point (raw data)(top image) is subtracted from the strain curve, with the fixed collecting intervals during experiments. For further noise analysis, I need to pick up the noise event positions, which is the top point of each noise peak, as the image of the noise peak point selected (bottom image). Currently, I am picking up points manually. However, there are thousands points in more than 10 sets of experimental data. Therefore, I wonder whether anyone can help me to write a macro to solve this problem?
I need a macro that can pick up the point only when its value is higher than both of the previous point and the next point in the wave. (or the point, which is higher than both of left and right points in the image, is selected)
thanks a lot for everything and any help for this!






July 20, 2011 at 06:57 am - Permalink
noiseout[1,23] = (noisetest[p - 1] < noisetest[p] && noisetest[p] > noisetest[p + 1]) ? 1 : 0where noisetest is the noise wave and noiseout is a wave that has a value of "1" where a local maximum was found and zero otherwise. It is assumed (and an examination of your example seems to confirm) that endpoints are not considered to be candidates for maxima.
Note:
The values of 1 and 23 for "noiseout[1,23]" were based on noisetest being a 25 element wave. The values of 1 and 23 exclude the initial (point 0) and final (point 24) points from consideration as mixima. (Sorry for not fully explaining this assumption in the initial post.)
July 20, 2011 at 11:48 am - Permalink
thanks a lot for your help. That's almost what I need. Also, my friend have helped me to modify it based on your commends as below to obtain a new wave from those i as below.
July 20, 2011 at 09:48 am - Permalink
July 20, 2011 at 09:53 am - Permalink
The additional code is understandable in spirit, but it does have some issues. One of the first issues is performance-wise: by making "peakname" with zero points and then enlarging it by one point for each peak found, you are effectively doing a complete copy of the wave each time. If you only have a low number of peaks (hundreds or a couple of thousands), this might still be acceptably fast.
You can avoid this in two ways: running the peak finding loop twice, the first time just counting how many peaks there are, and then making a wave with the correct number of points and just filling it up. But this requires two loop traversals, which induces a performance penalty just by itself.
Another way is to allocate a wave that you know will have too many points, do the analysis, and then remove all the points that were unnecessary.
Also, this line:
peakname[numpnts(peakname)]=data[i]is an out-of-bounds error (i.e. you are assigning to a wave element that does not exist). You can see this by realizing that array indices in Igor start from zero and run up to [numpnts(peakname) - 1]. By default Igor stays silent on this, but it is still an error.
Keeping all these points in mind, here's an improved version of the code:
July 20, 2011 at 10:26 am - Permalink
Is the x-axis scaling critical to your work? With the above code you are assembling a collection of peak values, but losing any information on the x-axis location of those values. That is, unless I'm missing a subtle point here.
July 20, 2011 at 11:43 am - Permalink
July 20, 2011 at 11:55 am - Permalink