Loess smooth curve with large range

Share icon

I'm having difficulty fitting a smoothed curve to a Mie scattering function with the following command:

Loess/DEST=fitYWave /DFCT/SMTH=(0.2) srcWave=defmapqscatmap, factors={defmapqscatdiams}

The attached graph shows the output (and the two input waves are also attached). It doesn't seem to matter what parameters I give to Loess, I always end up missing the fit at small diameters. The object of the exercise is to come up with some curve which follows the overall shape of the blue curve, but which increases monotonically. I'm pretty sure the problem arises from using a least squares fit over such a huge range of Y values.

I've also tried using a low pass filter to smooth the curve, but that tends to result in undershooting at small diameters. I'm sure there must be something obvious I should be doing, but I really can't find it. Anyone? defmapqScatDiams.ibw (15.74 KB) defmapqScatMap.ibw (15.74 KB)
Loess is minimizing the absolute error over the Y range of your data. At really tiny Y values this error looks really big.

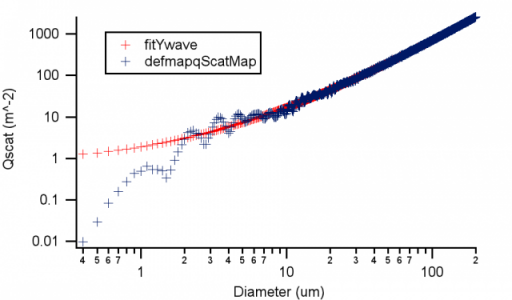
You may need to use Loess on the log of your data.

Better would be a curvefit to an actual model of your data. Loess is a rather brute-force approach; it knows nothing about the science underlying your data.

--Jim Prouty
Software Engineer, WaveMetrics, Inc.

June 9, 2011 at 12:09 pm - Permalink

Thanks Jim. I've ended up using a 15 point median smooth, calculating the scattering cross sections from the smallest diameter possible to give the median fit a head start for the region of interest, then replacing the first few points in the fit with the calculated data to improve the agreement at small diameters. It's a horrific kludge, but the science behind the data is highly non-linear so I guess it's the best I can come up with for now.

EDIT: To clarify, the blue line *is* a model of my data - I didn't show the actual data on the attached plot.

June 10, 2011 at 02:11 am - Permalink