Cutting a shape in an image

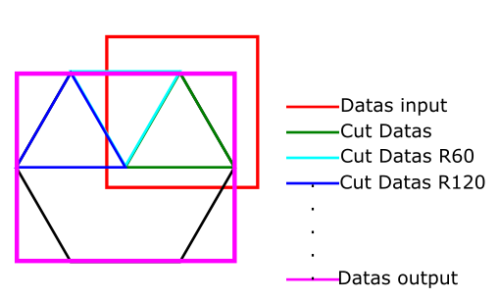
I assume you want to construct a Fermi surface out of ARPES data. You could create a new wave, only extract the data from your region of interest, then use ImageRotate to rotate this extracted data and finally paste it into a final output wave. BUT, this approach is highly convoluted and may reduce your data fidelity.

The more intelligent way to do this would be to first formulate a mathematical relation between the input data and the output data and then use interp2D for translation. In other words, you should think about a formula to map x,y of the input to x,y + angle of the output. This involves rotated mapping of coordinates along the seams of your triangles. Then you just need to do:

- create full output wave with proper scaling.

- do w_output = interp2D(w_input, x,y) where x and y are calculated according to your transformation formula.

If you could post some example data, we might be able to think about this together.

if you define the origin of output as the centre and the origin of input as the lower left corner of the ROI, then make a wave assignment where you go from output XY to polar coordinates, take mod(theta(pi/3)) and switch to input XY coordinates.

chozo's method with interp2d is doubtless better than a simple wave assignment. note that a 2D wave assignment will pick the closest point value without interpolation.

I'd approach the problem by creating a mask and then setting the image value to NaN outside the ROI.  Then use ImageInterpolate with an Affine transformation to rotate/shift/scale the data.  Note that if you are running a recent IP9 there is a further option for an inverse affine transformation.  Contact me through support@wavemetrics.com if you need further information.

A.G.

I use the interp2D function to perform the rotations and it works

ie: output=sum_i(interp2d(input,(x*cos(theta_i)-y*sin(theta_i)),(x*sin(theta_i)+y*cos(theta_i))).

However, my problem lies in the choice of x and y. I am trying to understand how to take only the pink data and then reconstruct my area. The formula above turns all my data, which results in an overlap.

p.s. : i use ip8

I see you use some user function sum_i() in your assignment. How about checking for a boundary condition of x,y to check whether they fall into you predefined triangle? You just have to implement some if checks to see whether x,y, falls within your ROI. If not you can return zero or NaN or a rotated version of your input wave. If you don't want to do this within sum_i(), you can also always fall back to writing a for-loop for stepping through your output wave and implement the boundary checks within this loop (I guess there are also more intelligent ways using Extract and/or MatrixOp, but this is the first thing I would try).

The sum_i is just a notation to explain the repetition of the interp function on each domain. Now the question concerns the bondaries.

another solution is to add the six domains rotated by 60 degrees, but here the overlaps must be normalized. An example of my data, on the left the raw data and on the right the data rotated with respect to the six folds axis.