
interpolating across NaNs in a 2-d matrix
I have a 2-D matrix which contains NaNs, and would like to interpolate to fill those NaNs. For now, my simple approach was to extract each column into a 1-D wave, do a linear interpolation and replace that column in the matrix. What are some better approaches to this? I could not find a suitable command to do this more directly.
Thanks
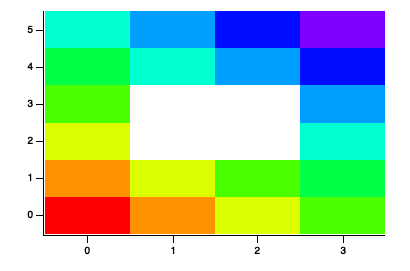
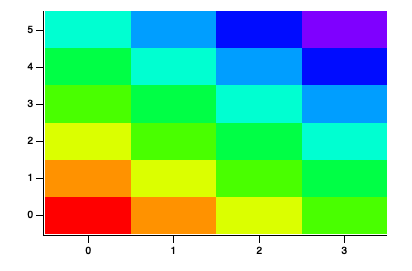







A simple approach is to convert the data that you have (surrounding the nans) into a triplet wave and then use ImageInterpolate Voronoi. Let me know if you need more details.
A.G.
February 1, 2021 at 11:11 am - Permalink
One approach might be to treat the matrix as an image wave. Use the RemoveBackground operation with a first order plane. Substitute the resulting values in the background matrix for the NaN values in this matrix.
February 1, 2021 at 11:21 am - Permalink
Isn't this what MatrixFilter NanZapMedian was designed to do?
MatrixFilter [/b=b /M=rank /N=n /P=p /R=roiWave /T] Method dataMatrix
The MatrixFilter operation performs one of several standard image filter type operations on the destination dataMatrix.
NanZapMedian n xn filter that only affects data points that are NaN. replaces them with the median of the n xn surrounding points. Unless /P is used, automatically cycles through matrix until all NaNs are gone or until cols *rows iterations.
February 1, 2021 at 06:43 pm - Permalink
MatrixFilter with zapMedian works better when you have isolated NaNs. In this case the NaNs seem contiguous so Voronoi interpolation is likely a better approach.
February 1, 2021 at 07:52 pm - Permalink