
Fitting constrains in multipeak fitting

Hi all,
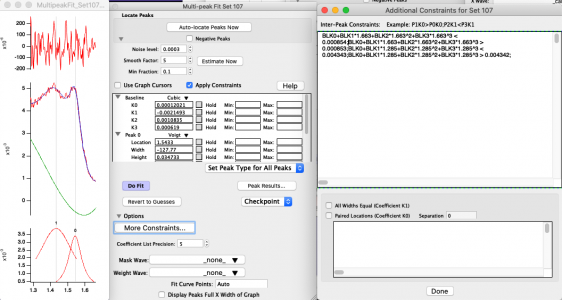
I am using the multi-peak fitting 2 package to fit a waveform with two Voigt function and a base function. I want to add a constraint that the base function needs to pass the endpoints. I couldn't find a place where I can put constraints consisting of linear combinations of baseline coefficients, so I just tried to put the following constraints in the "Inter peak constraints" textbox and it turns out it doesn't work...
So I am wondering whether I can achieve these constraints in the GUI interface? It is pretty handy and it would be great if I can avoid using function.
Another question is that is it possible to fix the Gaussian width in a Voigt function during the fitting?
Thanks,






First, would it be possible for you to provide a minimal example file with just this fit contained? We could help you more effectively then.
I am not sure if it is possible to constrain the cubic function to two points, but just looking at your input I do not see an (input) problem. Have you tried to constrain only one endpoint or first use a simpler constraint and then work your way up?
What are you trying to do by the way? Your fit looks a bit arbitrary to be honest. Do you have a physical model in mind for your background?
Your second question: No, with the current implementation it is not possible to fix just the Gauss with of a Voigt peak, since a highly accurate (and thus complex) algorithm for the peak shape is used. If you need this functionality, no matter what, then it is possible to write your own MPF peak shape function definition using the simpler VoigtPeak() function. Then you could provide a fixed value for the Gauss width alone.
I hope that helps.
March 30, 2020 at 01:08 am - Permalink
In case it is useful for someone, here are some pseudovoigt functions.
March 30, 2020 at 04:27 am - Permalink
In reply to First, would it be possible… by chozo
Hi chozo,
Thanks for your quick and helpful response. I have attached the example file.
I have indeed tested the textbox by using simpler constraints like P0K0 < P1K0 and it works. But whenever the constraint only includes parameters of one peak, it always does nothing. So I guess it can only work for constraints between peaks.
This cut is from a photoemission spectroscopy data( roughly density of states vs binding energy ), so in theory, I should use Shirley background instead of a cubic function. But the features that I am looking at are from the valence band so Shirley background may don't work in this case. So I am interested in whether a simple cubic function can mostly capture the background.
As for the second question, I will look into this Voigtpeak function and thanks for your advice.
March 30, 2020 at 08:03 am - Permalink
In principle, you can write a fitting function that takes Gauss width and shape parameter as fit coefficients. In fact, there is an example of such a fitting function in the documentation for Igor 8's VoigtFunc function. If that were the peak shape function in MPF2, then you could simply set and hold the Gaussian width. I have not tried to adapt the fitting function in that documentation for use in MPF2, but it should be possible. Getting all the parts of an MPF2 peak function working correctly is challenging, but possible. Before the 2 version of Multipeak Fit it was virtually impossible to add your own peak function.
You are right- there is presently no provision for including baseline parameters in constraints.
I don't know if it will help, but I once created an arc tangent baseline function for a customer. I never integrated it into MPF2 because it requires you to manually enter initial guesses for it. I have attached two procedure files; one implements the atan baseline, the other has a simple loader to start up MPF2 and load the atan baseline procedure file. Put the baseline procedure into User Procedures and the loader file in Igor Procedures. You can find those folders from Help->Show Igor Pro User Files Folder.
March 30, 2020 at 11:55 am - Permalink
The constraints for the baseline are working OK, but it is very fiddly to set usable constraints. First you have to know that the real x values from your raw data have no meaning for the calculation of the cubic function. Here, the x values always get re-scaled to the range -1 (beginning of your fit range) to +1 (end of your fit range). Your constraints would thus need to look like this:
BLK0-BLK1-BLK2-BLK3>0.00434
BLK0-BLK1-BLK2-BLK3<0.00434
BLK0+BLK1+BLK2+BLK3>0.000854
BLK0+BLK1+BLK2+BLK3<0.000854
I got some reasonable result out of this (see attached file), but only with Gaussians, as the Voigt peaks would run off in all directions. Also, the constraint for the left edge does not get obeyed really. Maybe this one is overridden by the right constraint, idk.
To be honest, this approach is so far from reality that you would be better off to subtract a Shirley background before attempting to fit anything. I have a GUI for subtracting background and could create a project here on IgorExchange if there is interest.
March 30, 2020 at 11:13 pm - Permalink
And in working with chozo, I said something that caused him to remove a statement to the effect of, "rumors have it that Igor 9 will include a Shirley background in MPF2". I regret saying that to him; my intent was to make sure that we didn't promise something that we failed to deliver, like a beta date for IP 9. Especially since COVID19 has upset life, we are reluctant to make *any* promises at all. In fact, the WaveMetrics engineers are working from home, and progressing on Igor 9 for a beta to start... sometime.
In fact, chozo is generously donating his time to make substantial improvements to MPF2. What working from home will do to a fellow :) I would say this is way better than spending all his free time binging the latest season of West World!
I would like to say that the fellow behind the "chozo" screen name is a very smart guy!
April 1, 2020 at 11:45 am - Permalink