Force Input Control Rounding on SetVariables

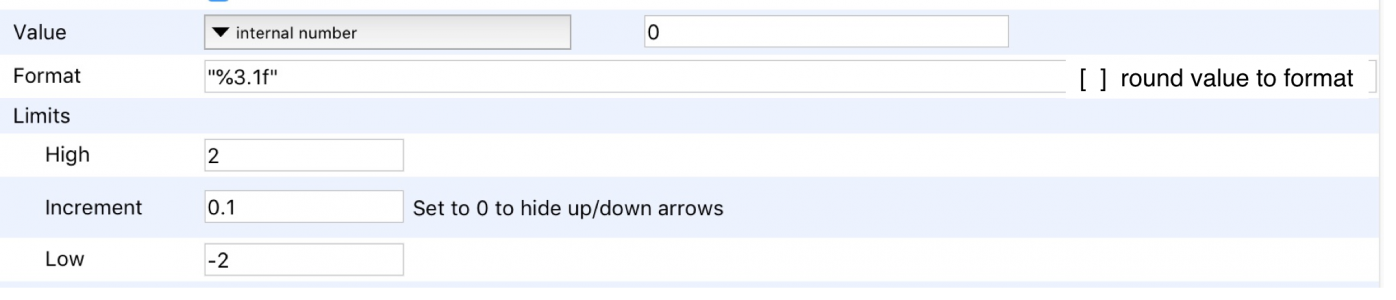
My expectation would be bug reports of values that weren't quite what people thought they should get. We get bug reports on arithmetic in a steady trickle.

With this control panel:

This action proc does what you want:

You still don't get exact values, of course. This "rounding" results in slightly different values than simply incrementing by the digital equivalent of 0.1, so the results in some cases change the greater-than and less-than relationships to the intended exact decimal number:

  dval = -2; sval = -2.0; rvalue = -2
  dval = -1.8999999999999999; sval = -1.9; rvalue = -1.8999999999999999
  dval = -1.7999999999999998; sval = -1.8; rvalue = -1.8
  dval = -1.7; sval = -1.7; rvalue = -1.7
  dval = -1.5999999999999999; sval = -1.6; rvalue = -1.6000000000000001
  dval = -1.5; sval = -1.5; rvalue = -1.5
  dval = -1.3999999999999999; sval = -1.4; rvalue = -1.3999999999999999
  dval = -1.2999999999999998; sval = -1.3; rvalue = -1.3
  dval = -1.2; sval = -1.2; rvalue = -1.2
  dval = -1.0999999999999999; sval = -1.1; rvalue = -1.1000000000000001
  dval = -1; sval = -1.0; rvalue = -1
  dval = -0.90000000000000002; sval = -0.9; rvalue = -0.90000000000000002
  dval = -0.80000000000000004; sval = -0.8; rvalue = -0.80000000000000004
  dval = -0.70000000000000007; sval = -0.7; rvalue = -0.69999999999999996
  dval = -0.59999999999999998; sval = -0.6; rvalue = -0.59999999999999998
  dval = -0.5; sval = -0.5; rvalue = -0.5
  dval = -0.40000000000000002; sval = -0.4; rvalue = -0.40000000000000002
  dval = -0.30000000000000004; sval = -0.3; rvalue = -0.29999999999999999
  dval = -0.19999999999999998; sval = -0.2; rvalue = -0.20000000000000001
  dval = -0.10000000000000001; sval = -0.1; rvalue = -0.10000000000000001
  dval = 0; sval = 0.0; rvalue = 0
  dval = 0.10000000000000001; sval = 0.1; rvalue = 0.10000000000000001
  dval = 0.20000000000000001; sval = 0.2; rvalue = 0.20000000000000001
  dval = 0.30000000000000004; sval = 0.3; rvalue = 0.29999999999999999
  dval = 0.40000000000000002; sval = 0.4; rvalue = 0.40000000000000002
  dval = 0.5; sval = 0.5; rvalue = 0.5
  dval = 0.59999999999999998; sval = 0.6; rvalue = 0.59999999999999998
  dval = 0.69999999999999996; sval = 0.7; rvalue = 0.69999999999999996
  dval = 0.79999999999999993; sval = 0.8; rvalue = 0.80000000000000004
  dval = 0.90000000000000002; sval = 0.9; rvalue = 0.90000000000000002
  dval = 1; sval = 1.0; rvalue = 1
  dval = 1.1000000000000001; sval = 1.1; rvalue = 1.1000000000000001
  dval = 1.2000000000000002; sval = 1.2; rvalue = 1.2
  dval = 1.3; sval = 1.3; rvalue = 1.3
  dval = 1.4000000000000001; sval = 1.4; rvalue = 1.3999999999999999
  dval = 1.5; sval = 1.5; rvalue = 1.5
  dval = 1.6000000000000001; sval = 1.6; rvalue = 1.6000000000000001
  dval = 1.7000000000000002; sval = 1.7; rvalue = 1.7
  dval = 1.8; sval = 1.8; rvalue = 1.8
  dval = 1.9000000000000001; sval = 1.9; rvalue = 1.8999999999999999
  dval = 2; sval = 2.0; rvalue = 2

So to summarize, I think trying to round would result in unexpected results just as much as not rounding. You can implement your own rounding, and get a result that you can inspect in detail rather than burying it in our source code. And you can adjust your rounding to get the results you need.

Why can't you just do it in the gui control procedure?

Fair enough.

This does force one to think explicitly about what is displayed in the panel versus what is actually stored/read for use.

But wait! You have sva.sval! That is in the format of the panel. Ok, this may do it.

In any case, I see that I may need to refresh the setvariable to force the increment to be exactly what I want rather than the rounding at zero problem going from ± 0.1 -> 0).

Thanks!

Yes, you can set the SetVariable value from within the action proc when the event is one of the "value changed" events. I recently had to fix that so I know it works now :)

So, let me try to summarize all this. Consider the case where you want a setvariable control to increment from -2 to 2 in 0.1 steps. You want the steps to be EXACTLY 0.1.

You have two ways to make this happen within a SetVariableControl structure function

Method I - Read sval

• Use SetVariable ... format="%2.1f" to define the format of the string in the setvariable display
• Ignore sva.dval
• Read sva.sval as a string ... It will have the desired format already rounded to the decimal place desired
• Use str2num to convert the string to a value

Method II - Read dval

• Use SetVariable ... format="%2.1f" to define the format of the string in the setvariable display
• Ignore sva.sval
• Read sva.dval as variable ... It will have floating point precision errors (i.e. it will not be EXACT as desired)
• Use an appropriate rounding method to force the variable to the desired decimal place

Of the two methods, the first seems the easiest.

When you wish to read the panel value using ControlInfo, you are out of luck with Method I. The ONLY way to force the value from ControlInfo on a setvariable is to use the approach below where MyRoundedValue is a function to force the value to a given precision.

My request was to have a checkbox to make the rounding happen behind the scenes so that ControlInfo would automatically format v_value as it was read by ControlInfo.

In this regard, I might amend my feature request to this ...

---

I would like to have ControlInfo on a SetVariable also return a value V_FValue where V_FValue (or a more appropriate name) is the value formatted according to the format string provided in the settings. When the format string is empty, V_FValue is the same as V_Value.

---

Please note that method 1 doesn't result in an exact number either, unless you use the string notation in arithmetic (which is going to be really difficult, though not impossible). The conversion to floating-point has its own floating-point error. The simple fact is that 0.1 when represented as a sum of powers of 1/2 is an infinitely repeating fraction.

Oh! OK. I'm clearly not as clear on this as I thought.

Truthfully, now that I've had a week to go through this, I realize that my main issue is solved. I want to avoid the rounding errors in the DISPLAY of the number. Rather than showing 2.7x10^{-17}, I wanted 0.0. I fixed that by setting the format of the display number.

Otherwise, for internal calculations, I should also have realized that what I am asking is ... silly. For all the time I spend telling my students to think about the RELATIVE influence (uncertainty) of a factor, you would think it would have dawned on me that we are talking about a round off error that affects the actual value in a relative manner by ppm or less.

I respectfully withdraw my request.

Thanks for the patience to follow me down a rabbit hole and drag me back out. :-)

The whole business of floating-point truncation error can be really hard to wrap your head around. There are places in Igor's code where we go to great lengths to work around it in a sane way. Think about the edge values of histogram bins. What happens with a data value that is "equal" to a histogram bin edge where the bins are increments of (very nearly) 0.1...