
Adjusting baseline on multiple waves

Caravaneer
I'm new to Igor Pro, and I'd like to know if there's an established way to deal with my kind of problem.
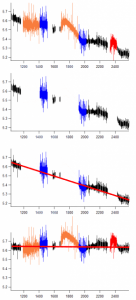
I have a data set which I want to modify in the following way: (please see image attached).
Essentially, it is a collection of waves that share the X axis, which is time. What I want to do is, I presume, "baseline adjustment", and there are few packages that do exactly that. However, the packages that I tried only deal with individual waves. In my case, the dataset in the example has 292 individual non-overlapping waves, each wave with the same delta of 0.0005 and different number of points, with some NaNs here and there, and with no data points in between each wave.
If I simply concatenate all the waves the X values for each wave and for missing data between waves are lost, and slope on my fit will be different.
As I see the problem now, I need to populate all the empty space in my graph with NaN points, and then concatenate waves, together with their NaN "spacers", to get one big wave that I can do baseline adjustment on. However after this I'd need to separate waves back to do analysis on the interesting parts (since I'm interested only in waves colored in orange).
I looked through the different topics, and what I could do is either append NaNs to each of 292 waves and then concatenate, which may result in some (acceptable) imprecision around the boundaries of each wave due to slight offset in time points - which I'm not sure how to approach. Or I'd need to do something like "Mass XY-pair to waveform" conversion, to interpolate all my data to one new wave - which I don't know how to do either (and I would like to avoid resampling altogether, if possible). Or maybe there is a way to do baseline adjustment on multiple waves at the same time, and I just don't know it yet - this would be best since I wouldn't lose individual waves that are convenient to analyze. Tony's Baselines_5.ipf package appears to be doing some of the work with "All in One" function fitting between two hand-placed markers, however it throws an error with waves that contain NaN points inside them.
I would appreciate any help!
Thanks.






Could you be a bit more specific about this? It should be possible to fit baselines to waves that contain NaNs, inasmuch as Igor's curve fitting allows this. It should even be tolerant of NaNs in the X-wave of X-Y plots, and of mismatched NaNs in X and Y waves.
If the baselines package refuses to fit baselines one-by-one, or if it fails ungracefully (i.e. with a runtime error) at any time, please let me know.
If you’re trying to do an ‘all in one’ baseline fit on waves with mismatched lengths, the baselines package will refuse to do that (but it shouldn’t throw an error).
April 9, 2018 at 09:11 am - Permalink
It's my mistake. Indeed, I have waves of 4 different lengths in this data set, but only one kind the wave (which is also the first in the dataset and the shortest) has no NaNs in it. I thought the reason was that other waves had NaNs in them, not that they were different length compared to the first wave.
The package does not "fail ungracefully", it performs everything with traces of one length and returns "Baselines all in one failed to fit [wave]" for the waves that have different length.
Edit: there is one behavior that may be considered a limitation (or a bug): if there's more than 64 traces in the graph, when trying to select "Baseline type" as "line between two cursors" and a 65th or any of the following traces in the "Data wave" list, then markers I and J do not appear. It is reversible if you select any trace between 1st and 64th.
April 9, 2018 at 09:43 am - Permalink
It also looks like you're fitting a line. Once you've done the fitting and have the fit coefficients, you can subtract the line from whichever data set you like, so you could duplicate the 'orange' data and do something like
OrangeDataBaselineSubtracted = OrangeData - coef0 - coef1*xor
OrangeDataBaselineSubtracted = OrangeData - coef0 - coef1*xwaveForOrangeDataApril 9, 2018 at 11:32 am - Permalink
I failed to reproduce this with many traces on a plot. Is there something different about the traces after the 64th?
April 9, 2018 at 11:49 am - Permalink
When I altered the total amount of traces displayed in one graph the number changed. I guess the "64" was a coincidence in the two graphs that I tested first. However the behavior is still there, I will try to upload a video and the experiment file.
I can not see any difference to the traces that could affect the module except for the wave naming. In the experiment that I upload if displaying all 101 waves in one graph first 11 can be made to show I and J markers; if other amount of consecutive waves is selected for display about 10 to 20% of waves that go in the start of the list show I and J markers (i.e. 5-7 for 50 waves, 3-6 for 30-31). If waves are selected for display randomly (i.e. not in consecutive order) the markers may not show at all, even for one wave on top of the list.
Video link:
https://drive.google.com/open?id=1FbjiX2grTFvAW76P6Q8EGIjsSw6_ZVSc
April 10, 2018 at 01:56 am - Permalink
I managed to produce a properly spaced single concatenated wave that I can fit with Baseline or Spline tools.
I gather that the "_coef" from Baseline tool provides slope and intercept, and "_BL" the values I need to add to my data for offset to 0 and slope correction?
How should I approach correcting my initial separated waves now that I have them spaced? Should I just add the "_BL" coefficients to everything?
April 10, 2018 at 05:24 am - Permalink
When you select the 'line between cursors' mode there's a pretty clunky and ad hoc algorithm that's used to decide where to put the cursors on the plot, based on the axis ranges and the data in the wave to be fit. It looks for the minimum data value in the first and last tenth of the range of the bottom axis, starting from the left axis. In your case, each wave takes up just a small part of the range of the x-axis, which is not a typical way to view data that you're trying to fit, and the algorithm fails.
If you plot the same wave in its own graph window, the cursors will appear as they should.
April 10, 2018 at 10:05 am - Permalink
If you do the fit yourself you will have access to the fit coefficients. So, for instance, if you fit a line to your data using the analysis->curve fitting menu, the coefficients will be recorded in the history and saved in a wave w_coef. You can use these to figure out what value to subtract from each point in your wave.
The baselines package uses CurveFit too, so you can look for that same w_coef wave after fitting a baseline to find the fit coefficients (for most of the fits - for the 'line between cursors' baseline you can instead look in the wavenote of the baseline to find the cursor positions).
I'm not sure exactly how you want to set up the fit and what you need as output, so it's hard to be more specific than that. It looks to me like you have sparse patches of data spread over some time period, and you wish to fit a linear trend through (all?) of the data, and then perhaps subtract that trend from each subset of data?
April 10, 2018 at 01:19 pm - Permalink