Inter-Peak constrain area with Voigt profiles

Share icon

Hi everybody,

I am analyzing diffraction patterns and usually fit the individual reflections with Voigt profiles. Actually I have two related questions concerning that:

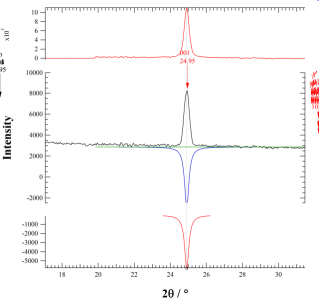
1. Was something changed with the Voigt functions implemented in Multi-Peak fit in one of the recent updates? The fitting used to work very well, but now something strange happens as i try to fit the peaks. I have attached a graph, where the resulting fit is obviously not very good ;-) After manually fiddling around and holding individual parameters it produces good fits but I didn't have issues like that when I did it the last time several month ago. No problems with Gauss or Lorentz profiles. Any ideas?

2. I usually have strongly overlapping reflections, so I need to fit them with two or three individual profiles. From other experiments I know their theoretical area ratio. Does anybody see a possibilty to use that and constrain the area, e.g. to say that the area of peak 1 should be twice the area of peak 2? I know that usually only linear depenences between peak parameters can be used, but is there maybe a version of a Voigt function, where the area is a a fit parameter? Probably the fact that the Voigt profile is a convolution of gaussian and lorentzian complicates things. If that is not pssible, is it maybe for pseduo-Voigt (linear combination of lor. and gauss) or at least gauss?

Thank you very much in advance!

Best regards,

Chris
In Multi-peak fit the Voigt profile is described in terms of "width","height" and "shape".
I don't think it will help to inter-constrain the height (if that is what you mean by amplitude), because the individual peak areas are also dependent on "width" and "shape".
In terms of the example above I would then have a peak 1 which has twice the height of peak 2, but I wouldn't constrain their respective areas, would I?

August 4, 2015 at 06:32 am - Permalink

Depends on their definitions:
If height is an amplitude, width a total width, and shape something like the width fraction of the Gaussian and Lorentzian contributions, you can use the proposed constraint (This would be the "nice" implementation.)
Maybe you want to test it on some calculated test data.
Another ansatz would involve to use your "own", normalized (Pseudo-)Voigt-function.
The convolution in the Voigt-function is not causing trouble if the underlying Lorentz- and Gauss-functions are normalized.
HJ

August 4, 2015 at 07:09 am - Permalink

ChrisZ wrote:
1. Was something changed with the Voigt functions implemented in Multi-Peak fit in one of the recent updates? The fitting used to work very well, but now something strange happens as i try to fit the peaks. I have attached a graph, where the resulting fit is obviously not very good ;-) After manually fiddling around and holding individual parameters it produces good fits but I didn't have issues like that when I did it the last time several month ago. No problems with Gauss or Lorentz profiles. Any ideas?

In a fit of over-zealousness, I made a change to the way constraints work in Igor 6.37 that was ill-advised. This affects Multipeak Fit because it uses an empty constraint to indicate that there should be no constraints. For Igor 6.38 I have made two changes: I backed out of my 6.37 change, and I added a check such that if the constraints are empty, it doesn't try to apply them. You can get these changes by downloading the latest nightly build: http://www.wavemetrics.net/Downloads/latest/

Quote:
2. I usually have strongly overlapping reflections, so I need to fit them with two or three individual profiles. From other experiments I know their theoretical area ratio. Does anybody see a possibilty to use that and constrain the area, e.g. to say that the area of peak 1 should be twice the area of peak 2? I know that usually only linear depenences between peak parameters can be used, but is there maybe a version of a Voigt function, where the area is a a fit parameter? Probably the fact that the Voigt profile is a convolution of gaussian and lorentzian complicates things. If that is not pssible, is it maybe for pseduo-Voigt (linear combination of lor. and gauss) or at least gauss?

You're right- it would be very difficult to implement. I think I've seen versions of the Voigt profile that have area as a coefficient, which would make it easier, but even so constraints don't work with division in the expressions. I have also seen "PseudoVoigt" profiles that simply add together a Gaussian and Lorentzian peak shape. That would make it easier to get the area, but a the expense of fitting something that isn't really a Voigt.

You might be able to come up with a user-defined fitting function that computes all the relevant areas, etc., and applies your constraints to it during fitting. But then you lose all the nice features of Multipeak Fit.


John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

August 10, 2015 at 03:15 pm - Permalink

HJDrescher wrote:
Depends on their definitions:
If height is an amplitude, width a total width, and shape something like the width fraction of the Gaussian and Lorentzian contributions, you can use the proposed constraint (This would be the "nice" implementation.)

The real amplitude is a complicated combination of the "height" coefficient and the shape coefficient. You can look in Windows->Procedure Windows->Peak Functions 2.ipf to see how the area and height are computed. See the function VoigtPeakParams().

John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

August 10, 2015 at 03:18 pm - Permalink

Dear everyone,

I'm sorry to dig out this 'older' topic, but I figured it's better than creating a new one.

I am dealing with a similar issue as the TO, but I would be happy enough with tying peak heights and shapes between different peaks to each other - I just can't find out how to do so.
the 'Inter-Peak Constraints' doesn't allow for P3K2 = 0.75 * P1K2, because the 'constraint expression lacks a conditional parameter'.

Reading through the help file and the forum didn't really help me out, and I was not adept enough to link those values to separate variables that two peaks should have in common.
However, I found a workaround by typing P3K2<=0.75*P1K2;P3K2>=0.75*P1K2 in the constraints field.
I do not trust this solution since I can imagine more than one way this ruins the code. Since I do get results with tied parameters the author might have taken care of that, though.

Finally my question: Is this the only way to do it? Is there an official way which I've missed?

Thanks for any help in advance.

September 3, 2015 at 04:42 am - Permalink

I am totally not knowledgeable about the internals of the constraints code (haven't worked with fitting for quite a while), but the equality operator is usually == so writing P3K2 == 0.75 * P1K2 might work. Note, that you will likely run into floating point rounding errors this way, and defining an interval is always a much safer approach.

September 3, 2015 at 05:06 am - Permalink

chozo wrote:
I am totally not knowledgeable about the internals of the constraints code (haven't worked with fitting for quite a while), but the equality operator is usually == so writing P3K2 == 0.75 * P1K2 might work. Note, that you will likely run into floating point rounding errors this way, and defining an interval is always a much safer approach.

Thanks for your swift reply, chozo.
While I didn't even think about using the comparison/conditional operator (obvious mistake) because I thought the value should be 'set' and not 'compared', it sadly yielded the same response about the lack of a conditional operator. For the moment, and because of your floating point comment, I will define a small interval around the target variable.

On a personal note: I've read through your conversation from 2010 about extending the MPF-tool partly to what it is today. Thanks for all the efforts you put into this. And (while i'm at it) also to johnweeks and nhyde for the devoted user support.

September 3, 2015 at 06:28 am - Permalink

Daniel G wrote:
I am dealing with a similar issue as the TO, but I would be happy enough with tying peak heights and shapes between different peaks to each other - I just can't find out how to do so.
the 'Inter-Peak Constraints' doesn't allow for P3K2 = 0.75 * P1K2, because the 'constraint expression lacks a conditional parameter'.

Reading through the help file and the forum didn't really help me out, and I was not adept enough to link those values to separate variables that two peaks should have in common.
However, I found a workaround by typing P3K2<=0.75*P1K2;P3K2>=0.75*P1K2 in the constraints field.
I do not trust this solution since I can imagine more than one way this ruins the code. Since I do get results with tied parameters the author might have taken care of that, though.

Finally my question: Is this the only way to do it? Is there an official way which I've missed?

What you are trying to get is an "equality constraint". Igor curve fitting doesn't do that, except for holding parameter values.
The only way to achieve an equality constraint is just what you came up with- two constraints that together can only be achieved with equality.

John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

September 3, 2015 at 10:30 am - Permalink

I am in a similar position of trying to fit Voigt functions to diffraction profiles using the MPF packages, but have a slightly different question.

I need to constrain both the shapes of the peaks and the inter-peak distances. From what I have found, I can constrain the shapes using MPF 1.4 and selecting "1 width" or "1 shape" and constrain the inter-peak distances using the dialog box in MPF 2. Is there a way to implement both of these constraints at once in either version of the MPF package?

Thanks!

September 30, 2015 at 11:18 am - Permalink

The only way to constrain the shapes to be all the same would something similar to the constraint that requests that the shape be both larger than, say, peak0 shape and also smaller. The expressions would be
p1k3 > p0k3;p1k3<p0k3;

which will be a big pain to create for even a moderate number of peaks.

And those can be combined with inter-peak distance constraints, of course. A yet bigger pain...

John Weeks
WaveMetrics, Inc.
support@wavemetrics.com

September 30, 2015 at 12:32 pm - Permalink