
Weighted fits of user defined functions

psingh8
Hello,
I'm a fairly experienced Igor user and good at math, but this issue is vexing me. I have a user defined function of f(x) = y0+Ax^(pow)+Bx where y0, A, B, and pow are fitted parameters. I'm comparing my fitted data with and without weighting. I would assume that without weighting, my weight wave would be equal to 1.
When I perform the fit without declaring a weight wave (no /W flag and no /I flag) I get a set of parameters equal to those with the weight wave = 1. However, the std dev of the coefficient values are all larger by a factor of 2500.
Puneet
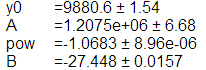
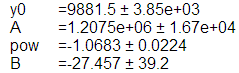

Forum

Support
Gallery
Igor Pro 9
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More






When you do a fit with a weighting wave, Igor believes that you are being honest about your measurement errors and computes the sigmas on that basis.
Without the weighting wave, the residuals are used to (do the same as) compute an estimate of your measurement errors. Apparently weights of 1 are a gross underestimate of the measurement errors?
March 16, 2020 at 05:19 pm - Permalink
Hi John,
Yes they are. Having a constant weighting wave made my code a little easier. Do you know what I can use as the weighting wave to get the same values?
Puneet
March 16, 2020 at 05:23 pm - Permalink
I found that making the weight wave = 2500 gave me the same values. The fact that its a round number and the same for each coefficients makes me think it has to do with the number of points in my fitting wave which is 10.
March 16, 2020 at 05:41 pm - Permalink
Exactly the same? I would guess that the "correct" value of the weight would be V_chisq/(N-M) where N is number of data points and M is number of fit coefficients. But if you do that, of course, you have used the chi-square value to estimate the weighting, which invalidates using chi-square as a goodness-of-fit estimator.
Possibly you are trying to do something along the lines that are covered in this section of the curve fitting help: DisplayHelpTopic "Proportional Weighting"
Also keep in mind that your equation is highly nonlinear, which means that all this weighting and chi-square and coefficient sigma stuff is just a linearized approximation. You should really use something like the bootstrap or jackknife, which are difficult to use.
March 17, 2020 at 03:39 pm - Permalink