Simultaneous Data Fitting to User-Defined Function

Share icon

Fri, 05/06/2016 - 01:10 pm

Hi there,

I'm trying to write an Igor Procedure that will allow me to do something similar to what the Batch Fitting feature .

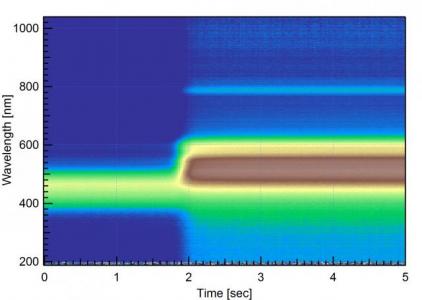
I've attached an image of how my data looks like after I run the import code. Basically, I have a set of absorbance data collected over time. Time(s) on the x-axis, wavelength(nm) on the y-axis, and absorbance intensity on the z-axis. The first problem is that I need wavelength to be in units of eV instead of nm. I wrote a little procedure that works on 1D waves, but I have no idea on how to approach this for a 2D wave.

This is the code I use to import my data and graph the resulting waves as an image. As a side note, I have been trying to plot my data using the Gizmo feature but my data doesn't seem to be compatible with it? It'd be nice to be able to show how the data changes as a surface rather than by a gradient.
#pragma rtGlobals=3     // Use modern global access method and strict wave access.

//imports a time series of UV-vis spectra acquired via the Ocean Optics spectrometer/software
Function ImportTemporalSpectra(name, [d])
    String name //name of data set
    Variable d //display the imported data
    String CurrentFolder=GetDataFolder(1)
    String fname="root:"+name
    String wname
    NewDataFolder/o/s $fname
   
    //Load 2D data
    wname="C=2;N="+name+";"
    LoadWave/Q/J/M/U={1,2,1,2}/B=wname/A/K=0/L={15,16,0,1,0}/O/N/D
    WAVE spec=$(name), lambda=$("CP_"+name), timeData=$("RP_"+name)
    duplicate/d/o lambda, $(name+"_L")
    duplicate/d/o timeData, $(name+"_T")
    duplicate/d/o spec $(name+"_raw")
    WAVE spec=$(name+"_raw"), spec2=$(name), lambda=$(name+"_L"), timeData=$(name+"_T")
    Killwaves $("CP_"+name), $("RP_"+name)
   

    //Scale data for time
    Duplicate/d/o timeData dt
    Differentiate dt
    wavestats/q dt
    print V_avg
    variable avgDt=V_avg/1000 //convert to seconds from ms
    setscale/p x, 0, avgDt, spec, spec2
   
    //interpolate data for wavelength
    Duplicate/d/o lambda dummyspecRaw, dummyspecScaled
    variable firstLambda=lambda[0]
    variable lastLambda=lambda[numpnts(lambda)-1]
    setscale/I y, firstLambda, lastLambda, spec2
    setscale/I x, firstLambda, lastLambda, dummyspecScaled
    Variable i
    For(i=0; i<numpnts(timedata); i+=1 )
        multithread dummyspecRaw=spec[i][p]
        multithread dummyspecScaled=interp(x, lambda, dummyspecRaw)
        multithread spec2[i][]=dummyspecScaled[q]
        If( i>0 && mod(i,2000)==0 )
            print "Processing time index="+num2str(i)
        endif
    endfor
//  Killwaves dummyspecRaw, dummyspecScaled, dt
   
    If( d )
        dowindow/F $name
        If( V_Flag==0 )
            display /W=(10,50,360,300) /N=$name as name
            appendimage spec2
            ModifyGraph grid=2,tick=2,minor=1,standoff=0
            Label left "Wavelength [nm]"
            Label bottom "Time [sec]"
            ModifyGraph margin(left)=36,margin(bottom)=29,margin(top)=14,margin(right)=14
            ModifyImage $name ctab={0,1.5,Terrain,0}
        endif
    endif
   
    SetDataFolder $CurrentFolder
End


The second problem involves fitting my data to a custom-function and extract the various fitting parameters over time. At the moment, I can fit single spectra at a time. However, I have hundreds and sometimes thousands of spectra for every experiment and would like to automate that process if possible. I completed the Batch Fitting demo and tried it on my data but I keep getting NaN. The goal is to have a procedure that allows me to get graphs that show how the various fitting parameters change with time.

This is the code I'm using to define the fit-function:

#pragma rtGlobals=3     // Use modern global access method and strict wave access.

Function Spanov5(w,E) : FitFunc

    Wave w
    Variable E
    Variable m,n
    Variable Amplitude
    Variable Gaussian
    Variable Total
   
    //CurveFitDialog/ Coefficients 6
    //CurveFitDialog/ lim=maximum vibrational level --> At most 5
    //CurveFitDialog/ S=Huang-Rhys Factor=w[0] --> Set equal to 1.0
    //CurveFitDialog/ W=Exciton Bandwidth=w[1]
    //CurveFitDialog/ Ep= Intermolecular Vibrational Energy=w[2] --> Set equal to 0.179eV
    //CurveFitDialog/ E_0=0-0 Vibrational Transition Energy=w[3]
    //CurveFitDialog/ h= Gaussian Width=w[4]
    //CurveFitDialog/ m,n=Different Vibrational Levels-->Range from 0 to at most 3
    //Curve Fit Dialog/ w[5]=lim i.e. maximum value of m and n
    //Curve Fit DIialo/ w[6]=Amplitude parameter
           
    m=0 //Used a do-while loop to control the series summation
    do
        n=0
        do
            if (m!=n)   //Transition can't occur in same vibrational level     
               
                Amplitude=(exp(-w[0])*(w[0])^m)/(factorial(m))*((1 - ((w[1]*exp(-w[0]))/(2*w[2]))*(((w[0])^n)/(factorial(n)*(n-m))))^2)    
               
//              Gaussian=(1/(w[4]*sqrt(2*Pi)))*exp(-(((E-w[3]-m*w[2]-.5*w[1]*((w[0])^m)*exp(-w[0]))^2)/(2*(w[4])^2)))

                Gaussian=exp(-(((E-w[3]-m*w[2]-.5*w[1]*((w[0])^m)*exp(-w[0]))^2)/(2*(w[4])^2)))
                Total+= w[6]*Amplitude*Gaussian
//              print amplitude, Gaussian
            endif
           
            n+=1
           
        while(n<=w[5])
       
        m+=1
   
    while(m<=w[5])
           
    return Total
End


I'm attaching a .txt file that has the raw data, Notepad crashes while trying to open it, but Notepad++ can process it just fine. It's not the best data set, but it's the only one I currently have the adheres to the 9MB limit. Also, it is really important that the x-axis is in units of eV(electronvolts) and not nm(nanometers) when fitting the data. When I import my data from the spectrometer the absorbance is saved as a function of wavelength. At the moment, I'm manually plotting absorbance vs eV.

Any suggestions/help is very much appreciated.

Thanks.



 P3HT-FANOFF-25C-CHCl3-50mmps_Absorbance_20-27-11-533.txt
I might address what I see in your post from a number of perspectives. First, with regard to the overall approach to peak fitting of spectra, I have a direct question. Why are you interpolating the raw data in time and wavelength? Are you thinking that you need to take this approach to use a fit function? Do you realize that you are loosing precision (resolution) by doing these interpolations? Do you appreciate that fit functions in Igor Pro can be written to take y and x wave references?

Secondly, as for the question about converting the scale from wavelength to energy, use h*nu = h*c / lambda = E. Add something equivalent to these lines appropriately in your loading function ...

firstenergy =h*c/lastLambda
lastenergy = h*c/firstLambda
... scale accordingly


FWIW, when I work with fitting spectra, I do not convert the raw scales unless the conversion is just an integer factor. I try as best possible to fit the raw data as given and then convert peak parameters to other physical units as needed. I have a host of reasons why. First, the bookkeeping involved in converting scales can be tedious and prone to errors. Secondly, the conversion can be non-linear (as your case is). Thirdly, it can cause round-off errors or loss of precision in the raw data itself. All of these factors are more trouble than just working with the raw data and writing robust routines to convert peak parameters and the fitting constants themselves as needed. For example, 0.179 eV = 6926.49 nm.

http://www.entorb.net/tools/nm-eV-Converter.php

As for the Gizmo and surface plotting, I am old-school here. I actually like your 2-D image plot better. Just use grayscale intensity rather than rainbow colors. Or, for a potentially really cool and physically meaningful image, plot the wavelength as different colors and peak intensity as black to white. Peak intensity at a given wavelength at a specific time means more than the color at a specific time. As it is now, the colors are the only real confusing part of this image.

I have some other suggestions for the coding. But let's discuss the spectroscopy and general approach first if you don't mind.

--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAH

May 6, 2016 at 05:30 pm - Permalink

What is the magnitude of the error/imprecision that is introduced by interpolating? I have noticed that my data is slightly red-shifted relative to what the literature states it should be. Could it be an artifact of the loading procedure?

The reason I interpolated the data with respect to wavelength is because I thought it would help reduce variability between data collection due to drift from my light source. Similarly, I interpolate my data with respect to time because my instrument fluctuates quite a bit when collecting data at very fast collection rates. I would be happy to learn of a different approach you may have in mind.

I'm not sure what you mean by giving my fit function "x wave and y wave references". I thought I was restricted to an input wave and a parameter wave? Otherwise, I would need something more advanced like Structure function right?

For the nm to eV conversion, I'm using the following simple formula:

eV = 1239/lambda(nm) i.e. 1239/6926.49=0.179eV

My original code produces a plot with wavelength, time and absorbance. I tried to add to that code a couple lines to make it produce a second plot that plots eV, time and absorbance instead. Unfortunately, now both of my graphs look silly. Here is the modified code:

#pragma rtGlobals=3     // Use modern global access method and strict wave access.

//imports a time series of UV-vis spectra acquired via the Ocean Optics spectrometer/software
Function ImportTimeAbsv3(name, [d])
    String name //name of data set
    Variable d //display the imported data
    String CurrentFolder=GetDataFolder(1)
    String fname="root:"+name
    String wname
    NewDataFolder/o/s $fname
   
    //Load 2D data
    wname="C=2;N="+name+";"
    LoadWave/Q/J/M/U={1,2,1,2}/B=wname/A/K=0/L={15,16,0,1,0}/O/N/D
    WAVE spec=$(name), lambda=$("CP_"+name), timeData=$("RP_"+name)
    duplicate/d/o lambda, $(name+"_L")
    duplicate/d/o timeData, $(name+"_T")
    duplicate/d/o spec $(name+"_raw")
    WAVE spec=$(name+"_raw"), spec2=$(name), spec3=$(name), lambda=$(name+"_L"), timeData=$(name+"_T")
    Killwaves $("CP_"+name), $("RP_"+name)
   

    //Scale data for time
    Duplicate/d/o timeData dt
    Differentiate dt
    wavestats/q dt
    print V_avg
    variable avgDt=V_avg/1000 //convert to seconds from ms
    setscale/p x, 0, avgDt, spec, spec2,spec3
   
    //interpolate data for wavelength
    Duplicate/d/o lambda dummyspecRaw, dummyspecScaled
    variable firstLambda=lambda[0]
    variable lastLambda=lambda[numpnts(lambda)-1]
    setscale/I y, firstLambda, lastLambda, spec2
    setscale/I x, firstLambda, lastLambda, dummyspecScaled
   
    //Create eV wave from wavelength wave
    Duplicate /d/o lambda dummyspecRaw, dummyspecScaled
    variable firstenergy=1239/lambda[0]
    variable lastenergy= 1239/lambda[numpnts(lambda)-1]
    setscale/I y, firstenergy,lastenergy,spec3
    setscale/I x, firstenergy,lastenergy,dummyspecScaled
   
    Variable i
    For(i=0; i<numpnts(timedata); i+=1 )
        multithread dummyspecRaw=spec[i][p]
        multithread dummyspecScaled=interp(x, lambda, dummyspecRaw)
        multithread spec2[i][]=dummyspecScaled[q]
        multithread spec3[i][]=dummyspecScaled[q]
        If( i>0 && mod(i,2000)==0 )
            print "Processing time index="+num2str(i)
        endif
    endfor
//  Killwaves dummyspecRaw, dummyspecScaled, dt

//Plot Wavelength,Time, and Absorbance
    If( d )
        dowindow/F $name
        If( V_Flag==0 )
            display /W=(10,50,360,300) /N=$name as name
            appendimage spec2
            ModifyGraph grid=2,tick=2,minor=1,standoff=0
            Label left "Wavelength [nm]"
            Label bottom "Time [sec]"
            ModifyGraph margin(left)=36,margin(bottom)=29,margin(top)=14,margin(right)=14
            ModifyImage $name ctab={0,1.5,Terrain,0}
        endif
    endif
//Plot Energy, Time, and Absorbance
    If( d )
        dowindow/F $name
        If( V_Flag==0 )
            display /W=(10,50,360,300) /N=$name as name
            appendimage spec3
            ModifyGraph grid=2,tick=2,minor=1,standoff=0
            Label left "Energy [eV]"
            Label bottom "Time [sec]"
            ModifyGraph margin(left)=36,margin(bottom)=29,margin(top)=14,margin(right)=14
            ModifyImage $name ctab={0,1.5,Terrain,0}
        endif
    endif
   
    SetDataFolder $CurrentFolder
End


The result of the code is two identical graphs, and the data looks like noise. I've attached a picture of how it looks. It looks like it's doing the conversion to eV properly, however it seems to have lost the wavelength information and the absorbance info looks wrong as well. What am I overlooking?

I know how to change the color scale, to gray scale. I don't think I understand what you mean by plotting the wavelength as a different color. Could you explain further?

Thank you!
nonsense.jpg

May 7, 2016 at 02:27 pm - Permalink

vmmr5596 wrote:
What is the magnitude of the error/imprecision that is introduced by interpolating? I have noticed that my data is slightly red-shifted relative to what the literature states it should be. Could it be an artifact of the loading procedure?


I would think the imprecision is not a systematic offset error that is biased up or down in scale. I would propose it would cause line broadening at worst, though I may be mistaken.

Do a test. Find a peak in your interpolated data set. Find the same peak in the raw data. Determine the positions for both. Convert the positions to the same scale (wavelength or energy). Do they agree? By how much do they disagree? Is the interpolated data red-shifted?

vmmr5596 wrote:
The reason I interpolated the data with respect to wavelength is because I thought it would help reduce variability between data collection due to drift from my light source. Similarly, I interpolate my data with respect to time because my instrument fluctuates quite a bit when collecting data at very fast collection rates. I would be happy to learn of a different approach you may have in mind.


Interpolation in wavelength is not going to fix your problems of drift in the light source (intensity?). Interpolation only converts an unevenly-spaced scale to an evenly-spaced scale. It does not "renormalize" the data.

My suggestion here is to have either a more stable light source or take an independent measure of light intensity and renormalize the measurements against it. For this case, split the beam and use a second detector to track the light source intensity during the measurement of sample response.

Interpolation in time is a nice way to put every spectrum in the same step size apart for visual layout. Otherwise, since it distorts the raw data, I'd avoid doing data analysis with the interpolated data.

vmmr5596 wrote:
I'm not sure what you mean by giving my fit function "x wave and y wave references". I thought I was restricted to an input wave and a parameter wave? Otherwise, I would need something more advanced like Structure function right?


Yes.

vmmr5596 wrote:
For the nm to eV conversion, I'm using the following simple formula:

eV = 1239/lambda(nm) i.e. 1239/6926.49=0.179eV


You may want to realize this only gives a precision of 4 significant digits. You should use h*c to higher precision.

Also, first energy is determined at last lambda, not first lambda.

vmmr5596 wrote:
My original code produces a plot with wavelength, time and absorbance. I tried to add to that code a couple lines to make it produce a second plot that plots eV, time and absorbance instead. Unfortunately, now both of my graphs look silly. Here is the modified code:

...
    //interpolate data for wavelength
    Duplicate/d/o lambda dummyspecRaw, dummyspecScaled
    variable firstLambda=lambda[0]
    variable lastLambda=lambda[numpnts(lambda)-1]
    setscale/I y, firstLambda, lastLambda, spec2
    setscale/I x, firstLambda, lastLambda, dummyspecScaled // <-- you set the scale here
   
    //Create eV wave from wavelength wave
    Duplicate /d/o lambda dummyspecRaw, dummyspecScaled
    variable firstenergy=1239/lambda[0]
    variable lastenergy= 1239/lambda[numpnts(lambda)-1]
    setscale/I y, firstenergy,lastenergy,spec3
    setscale/I x, firstenergy,last energy,dummyspecScaled // <-- you reset the scale here
..


The result of the code is two identical graphs, and the data looks like noise.


As near as I can tell, one mistake is that you are using the same scale for both spec2 and spec3. This is because you have scaled dummyspecScaled to energy for both plots.

vmmr5596 wrote:
I know how to change the color scale, to gray scale. I don't think I understand what you mean by plotting the wavelength as a different color. Could you explain further?


You have to use an f(z) wave in a clever way. I'd have to think about this some more.

In the meantime, can you put a subset of your raw data in a ZIP archive. Post the full wavelength range and a time snap shot of perhaps a hundred spectra only, may be including the region where you see the sudden change (your spectra show the "turn on"). I'd like to try some things.


--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAH

May 7, 2016 at 03:00 pm - Permalink

I forgot to mention, the data is collected between 187nm to about 1038nm. The range that where I plan to do analysis/curve fitting is between 250nm and 750nm. The data is pretty noisy at the wavelength limits so don't worry about that.

May 7, 2016 at 03:38 pm - Permalink

I agree that you should do as much fitting as possible with the raw data before doing any transformations or interpolation. Otherwise you're asking for trouble.

I've also cobbled together some code for batch peak fitting for a similar application, so I revised it a bit for your data and attached the experiment here. I admit my procedure's not the cleanest, and it does not recognize x waves. My approach is to use the Multi Peak Fitting 2 package first to get a good multi-peak fit; in this example I just used Gaussians, but it's not too hard to do implement it with your own custom (Spanov) function. Then I fix certain fitting parameters and add constraints such that the fit doesn't go wild as it progresses.

For your data, first I used Excel to clean up the data -- transpose the rows/columns and discard anything outside approximately 250-750 nm. I imported each time interval into Igor as a separate 1D wave and set the x-scaling of all waves (start 256.5, delta 0.436; this is approximate because your wavelengths weren't exactly linearly spaced). Next I plotted an example spectrum, used multi-peak fitting to fit it, saved a peak-fitting checkpoint, and made sure that a later spectrum would fit appropriately when initialized using that checkpoint. I got decent results by fixing all peak locations, fixing peak widths except for the 550-nm peak, and letting heights vary.

Then I plotted all the spectra on one graph and ran my custom function which is based on the code in the "multi-peak fitting for igor programmers" section of the "Multi-peak Fitting 2 Help.ipf" documentation. This procedure grabs all the traces on the top graph and does multi-peak fitting on each one sequentially using the parameters that you set up in the checkpoint. In this case, I also had the function extract the peak intensities and 550-nm peak width to plot for you.
Hope this helps!
MultiSpectraFitting.pxp MultiSpectraFitting.jpg

May 11, 2016 at 03:25 pm - Permalink

Hi there,

When I load your .pxp file the .ipf is missing. Would you be able to upload that? I was actually reading into that this morning in the manual and would be curious to see your approach.

I had already tried the Peak Height vs time analysis that you showed. It gives a nice sigmoidal fit for the data. The plots that I'm actually trying to extract involve the fitting parameters graphed versus time (i.e. Exciton Bandwidth vs time, Transition Energy vs time, etc).

I used to do my analysis in Excel but I like IGOR much much better. I'm trying to avoid Excel if possible. :)

I'm currently trying to achieve the following:

1) Import the following data from the .txt file: Absorbance, time, and eV . I can import Absorbance, time and wavelength(nm) just fine as of now. Writing a procedure where the eV wave is generated during the import has been tricky to me so far.

2) Fit my custom function (Spanov5) simultaneously to all the spectra and extract information of how the parameters change with time. This is the action that I'm most interested in.

I'm also working on writing an Igor procedure that will allow me to remove the wavelength data that I don't need (i.e. only the data between 250nm and 750nm is imported) and that will allow me to perform a baseline correction (i.e. find the minimum absorbance value in a particular range of the data and add that value to the spectrum). I know that I could manually do both of those procedures in IGOR but I'd like to take advantage of the programming capabilities to automate some of the work since it would save LOTS of time in the long run.

Thanks for your help!

May 12, 2016 at 10:31 am - Permalink

Looking closer at your fitting function, I now see why you need to convert the data to be as a function of energy. I still recommend making the spectrum for each time step its own wave and also having a wave just containing the wavelengths, for example "lambdas". Then make a wave for the energy, say "energies." Then set energies=1239/lambdas. This sets you up nicely to use the built-in interpolation on each spectrum, for example:

Interpolate2/T=3/N=2000/F=0 energies, wave0

will create wave0_SS that automatically rescales the x dimensions of the final wave in the appropriate fashion. I set the number of data points to 2000 but you could make this higher if you want.

Now that you have a set of spectra that are scaled by energy, you can run the batch multi-peak fitting routine that I described above. I rewrote your Spanov5 fitting function to work with the Multi-Peak Fitting 2 package, and I've attached the necessary procedures here.

I don't really know the physics behind your experiment, so I couldn't make very reasonable guesses for the fitting parameters, but I've also attached an experiment where I used the Spanov5 fit function as well as a couple gaussians to fit your spectra series. I'm guessing my results are nonsense but it shows you the general idea.
MultiSpectraFittingEnergy.jpg MultiSpectraFittingEnergy.pxp BatchPeakFitting.ipf Spanov5peak.ipf

May 12, 2016 at 10:53 am - Permalink

Glad to see that ajleenheer has been able to help significantly here. I might comment on one statement though ...

ajleenheer wrote:
Looking closer at your fitting function, I now see why you need to convert the data to be as a function of energy.


I might wonder why the function cannot be modified in this way ...

Function Spanov5Lambda(ww,lambda)
     wave ww
     variable lambda

     variable eV = 1239.8 / lambda

      ... rest of fitting function here

end


I might also do something a bit more clever with matrix math rather than two do ... while loops, for example ...

variable np = w(5)
make/N=(np,np)/FREE nwwA
make/N=(np)/FREE nwwG
nwwA = exp(-w[0])*(w[0])^q)/(factorial(q))*((1 - ((w[1]*exp(-w[0]))/(2*w[2]))*(((w[0])^p)/(factorial(p)*(p-q))))^2
nwwG = exp(-(((eV-w[3]-p*w[2]-.5*w[1]*((w[0])^p)*exp(-w[0]))^2)/(2*(w[4])^2)))


Even though you will not use the n = m values, the computational overhead to test them (in do ... while loops) is larger than the overhead to compute them and then discard them later (by some clever math tricks). I have to ponder a bit more on how to do the Total calculation from this (likely via MatrixOP).

What these changes would mean for your work are ...

* Removes the need to covert during interpolation ... always a benefit for accuracy and precision
* Uses implicit math and MatrixOP ... always a significant benefit for speed
* Rewrites the function without the CurveFitDialog conventions ... requires you do your own coding

Finally, I'd have to suggest that you avoid the interpolation entirely by rewriting the fitting function to take two input waves, wwC (coefficients) and wwL (the lambda values). This would become ...

Function Spanov5IvL(wwC, wwL, pp)
    wave wwC, wwL
    variable pp

    variable eV = 1239.8 / wwL[pp]

    ... rest of fitting function here


The efforts that you can put up front to make these changes will offer significant improvements in accuracy, precision, and speed in return.

--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAH

May 14, 2016 at 11:58 am - Permalink

All good stuff from jjweimer. I didn't play around at all with optimizing the fitting function. It's probably a good idea to do the lambda-to-energy conversion in the fitting function rather than converting the spectral data; however, if you use my code, that won't directly work because my fitting routine expects just a scaled y wave and will not work as-is with a x- and y- wave.

jjweimer wrote:

The efforts that you can put up front to make these changes will offer significant improvements in accuracy, precision, and speed in return.


Just use your judgement about how "significant" the improvements will be by optimizing the Igor code. In my experience it's really easy to spend many hours working on Igor code to speed something up that may save you 10 minutes of number crunching over the course of a few months of experiments, and by that time you realize that your experiment needs to be different anyhow.

Honestly, I was surprised how fast the fitting worked even when using the do...while loops; I had expected it to be terrible. And I wouldn't worry too much about the loss of accuracy by interpolating -- with data as noisy as yours and so many fitting parameters (especially the exciton line width and gaussian broadening parameters), interpolating is the least of your worries if you do it properly.

May 16, 2016 at 07:41 am - Permalink

ajleenheer wrote:

It's probably a good idea to do the lambda-to-energy conversion in the fitting function rather than converting the spectral data; however, if you use my code, that won't directly work because my fitting routine expects just a scaled y wave and will not work as-is with a x- and y- wave.


Interpolating the original intensity vs lambda to a scaled intensity wave will give the desired y-wave as intensity with x as lambda. Then write the conversion inside the fitting function.

ajleenheer wrote:

Just use your judgement about how "significant" the improvements will be by optimizing the Igor code.


The attached experiment shows two rewritten functions with about a 10% - 20% speed increase. I still have to wrap my head around MatrixOP to get the off-diagonal math right. But, at this point, your statement about time invested vs speed increase kicks in.

ajleenheer wrote:

And I wouldn't worry too much about the loss of accuracy by interpolating -- with data as noisy as yours and so many fitting parameters (especially the exciton line width and gaussian broadening parameters), interpolating is the least of your worries if you do it properly.


Eventually, I'd be curious why not to use an x and y wave, since for example Multipeak Fitting supports it. It seems eventually that doing an interpolation is as much effort to get right as just plugging in an x-wave without interpolation.

--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAH
testspanov5.pxp

May 16, 2016 at 10:04 am - Permalink