Power Spectral Density with Window Function

Share icon

Hi everybody,

first, sorry for my english :)
I am trying to do some Fourier Analysis to some timeseries signals and recognized a problem, which I can't solve on my own.

For some testing I created a sin-wave using:
Make/D/N=128 sinus_test
sinus_test=sin(x)

Afterwards I plotted the PSD using
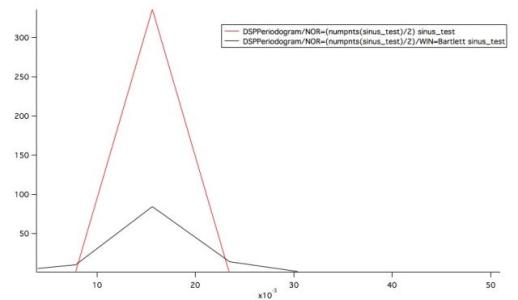
DSPPeriodogram/NOR=(numpnts(sinus_test)/2) sinus_test

The Normalization needs to be done, for comparing Variance of the time signal with the Integral over the Periodogram (Parseval Theorem).

Until now, everything works fine and the variance is identical to the Integral over the Periodogram.

Now I need to do some segmenting and applying a window Function and for that, I change the Syntax to:
DSPPeriodogram/NOR=(numpnts(sinus_test)/2)/WIN=Bartlett sinus_test

The Problem is shown in the attached image. The y-Values are much lower, than without the Window Function, and so the Integral isn't the same as the variance anymore.
So, I tried to fix it and changed some values in the nomralization term, which leeds to:
DSPPeriodogram/NOR=(numpnts(sinus_test)/8)/WIN=Bartlett sinus_test

This works in this sin case, but for me the mathematical sense is missing.

Perhaps someone of you could explain to me, in which way the normalization has to be changed, so that the Integral over the PSD stays the same?

Thanks a lot

Greets, Jens
Hello Jens,

If you want the normalization to compensate for the window function you can omit /NOR flag. Here is an example:

Make/O/D/N=128 sinus_test=sin(x)
DSPPeriodogram sinus_test
Duplicate/O W_Periodogram,firstWave
DSPPeriodogram/WIN=Bartlett sinus_test
Display firstWave,W_Periodogram


If you want to know the effect of the window function on a wave of the same length as your input, you can execute:
Make/O/D/N=128 norWave=1  // same length as your input
WindowFunction/Dest=winFuncWave Bartlett,norWave
MatrixOP/O aa=sum(winFuncWave*winFuncWave)/128


You can combine this with /NOR=0 and then apply any normalization you wish to the result of DSPPeriodogram.

I hope this helps,

A.G.
WaveMetrics, Inc.

November 19, 2012 at 11:49 am - Permalink

Hello,

thanks for your answer.
I don't know if I get your last point right and if this is what helps..
What I need to do is, Calculate the variance of a timeseries, do a FFT using PSDPeriodogram, integrate over the W_Periodogram output and this has to be the same as the variance of the timeseries. (until now,this works really fine with /NOR=(numpnts(winput)/2)).
But then I have to check the variance of my timeseries against the Integral of a segmented FFT with an underlying Window Function to get a Plot like in the attachment.
In my case I have a timeseries of N=4100, want to segment it in 30 half-overlapping segments.
I did this using:
DSPPeriodogram/NOR=(numpnts(winput)/2)/WIN=Bartlett/SEGN={128,64} winput

The Problem now is, that the variance of my timeseries is 115.8, the integral over the the W_Periodogram is 112.9 (this is just fine), but the Integral over the segmented Periodogram is only 1.26, with the term /NOR=(numpnts(winput)/2), and 60.4 without the normalization term and it needs to be nearly the same value as the other both.

Any ideas?

Thanks a lot

Greets Jens
periodogram_nor.jpg (26.22 KB) Periodogram_seg.jpg (20.1 KB)

November 20, 2012 at 03:07 am - Permalink

peeda85 wrote:
Hello,
I don't know if I get your last point right and if this is what helps..


That last point is crucial. Here is a test function that you can apply to a 1D wave. It prints out the variance and the sum of the periodogram after normalizations and corrections and illustrates the use of WindowFunction which I mentioned earlier.

Function foo(inwave,pointsInSegment)
    wave inwave
    Variable pointsInSegment
   
    DSPPeriodogram/Q/DLSG/NOR=(pointsInSegment*pointsInSegment/2)/SEGN={(pointsInSegment),(pointsInSegment/2)}/Win=bartlett inWave
    Wave W_Periodogram
   
    // small corrections for the first and last bin
      W_Periodogram[0] /= 2                                                          
      W_Periodogram[numpnts(W_Periodogram)-1] /=2  
       
    // now look at the window function:
    Make/Free/N=(pointsInSegment)/D norWave=1
    WindowFunction/Dest=winFuncWave Bartlett,norWave
    MatrixOP/O/Free aa=sum(winFuncWave*winFuncWave)/pointsInSegment
    Variable nor=1/aa[0]
    MatrixOP/O W_Periodogram=W_Periodogram*nor
    print sum(W_Periodogram),variance(inWave)
End


A couple of minor points here are the use of /DLSG flag and the bin corrections.

A.G.
WaveMetrics, Inc.

November 20, 2012 at 03:53 pm - Permalink