Function or operation or method to "transpose" a wave?

Share icon

I have a scaled wave of temperature versus composition T(z), where z goes from 0 to 1. I wish to map this to a scaled wave of composition versus temperature z(T). In cases where T may be above or below the values in T(z), I wish to set the wave z(T) to NaN.

This must be easier than iterating over the wave index in a for-loop with FindLevels??? Is there a function that would "transpose" the y-x values in a scaled wave based on boundaries. I'm thinking akin to this ...

TransposeWave/O/R=(xo,xf)/OR=NaN srcwave /D=destwave

Transpose the scaling of a 1-D wave with its values. Use /R for the start xo and end xf of the transposed scaling. Use /OR for the value to use when srcwave is outside the limits of xo to xf.

While I slug this through, does someone have a routine that they could share?

EDIT: I have a method with FindLevel that I can post. In the meantime, I attach an example of two graphs. The left is the "raw" T(z) data. The right is the generated z(T) data. Those who know isomorphous phase diagrams will recognize the left as solidus/liquidus or bubble point/dew point lines and the right as fractional solid (or liquid) using the lever rule. To generate the right plot, I needed to translate the T(z) lines to z(T) lines and do some algebra.

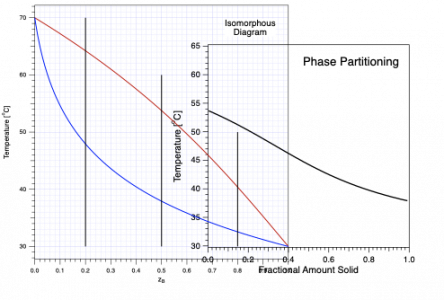
 example results desired

Can you accomplish what you want with Interpolate2? Here is an example that does a decent job, but I think it need some tweaking to properly handle the endpoints, and I haven't worried about NaN values.

make/O/N=50 Tz1=70-sqrt(p*30) //approximation of your first curve
make/O/N=50 Tz2=70-(p/8)^2 //approximation of your second curve
make/O/N=50 zFrac=p/50 //make an x wave (if it doesn't already exist)
make/O/N=200 Tvals=NaN //make a dummy temperature wave, just used for scaling
SetScale/I x 30,70,"", Tvals //set the scale of the destination waves to make later arithmetic easier
Duplicate/O Tvals zT1, zT2 //create the destination waves
Interpolate2/E=2/I=3/Y=zT1 Tz1, zFrac //interpolate the first
Interpolate2/E=2/I=3/Y=zT2 Tz2, zFrac //interpolate the second

The resulting waves "Tz1" and "Tz2" are interpolated transposed waves, with the same scaling so you can do the further arithmetic.

November 28, 2020 at 08:45 pm - Permalink

Thanks. I had not considered the interpolate operation or its corresponding function interp(...). But they do exactly what I need here.

November 30, 2020 at 09:21 am - Permalink