FindRoots issues

Share icon

First of all, this is what I'm trying to do: I want to optimize thermodynamic data which I need to calculate chemical equilibrium of a number of phases. Equilibrium is achieved when the Gibbs free energy G of two (or more) pure phases is identical at given temperature T and pressure P. I have defined a function "Gibbs", which returns the Gibbs free energy for a phase, e.g.:

G_phase1 = Gibbs(w1, T, P)

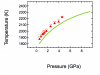
where w1 is a parameter wave containing thermodynamic data (8 variables) for phase1. Within Gibbs(w, T, P) there is already a call to Findroots to solve part of the free energy equation numerically. The attached figure shows the equilibrium curve between phase 1 and phase 2 with current thermodynamic properties. Now I want to fit the values in the parameter wave of phase2 to match the experimental brackets (red data on plot). I don't have an analytical expression for the equilibrium curve ( this is also constrained using Findroots), so I can't use regular curve fitting.

I define a set of 8 equations, like:

0 = Gibbs(w1, 1880, 0.5) - Gibbs(w2, 1880, 0.5)

etc, where T and P are chosen to be consistent with the experimental data and run it with Findroots by using the values in wave w2 as variables. The FindRoots call looks like this:

findroots  /X=guess, SolveThis, par


and the function containing the equations
function SolveThis(w, xW, yW)
    wave w, xW, yW

    wave w_phase2, w_phase1
   
    w_phase2[%V0] =xW[0]
    w_phase2[%K] =xW[1]
    w_phase2[%Kprime] =xW[2]
    w_phase2[%y0] =xW[3]
    w_phase2[%yprime] =xW[4]
    w_phase2[%Cv] =xW[5]
    w_phase2[%S0] =xW[6]
    w_phase2[%F0] =xW[7]

    yW[0] =  Gibbs(w_phase1, w[%T][0], w[%P][0]) - Gibbs(w_phase2, w[%T][0],w[%P][0])  
    yW[1] =  Gibbs(w_phase1, w[%T][1], w[%P][1]) - Gibbs(w_phase2, w[%T][1],w[%P][1])
    yW[2] =  Gibbs(w_phase1, w[%T][2], w[%P][2]) - Gibbs(w_phase2, w[%T][2],w[%P][2])  
        yW[3] =  Gibbs(w_phase1, w[%T][3], w[%P][3]) - Gibbs(w_phase2, w[%T][3],w[%P][3])  
        yW[4] =  Gibbs(w_phase1, w[%T][4], w[%P][4]) - Gibbs(w_phase2, w[%T][4],w[%P][4])  
        yW[5] =  Gibbs(w_phase1, w[%T][5], w[%P][5]) - Gibbs(w_phase2, w[%T][5],w[%P][5])  
        yW[6] =  Gibbs(w_phase1, w[%T][6], w[%P][6]) - Gibbs(w_phase2, w[%T][6],w[%P][6])    
        yW[7] =  Gibbs(w_phase1, w[%T][7], w[%P][7]) - Gibbs(w_phase2, w[%T][7],w[%P][7])
end


Par is a wave with 8 columns containing the temperature and pressure that are being addressed using dimension labels. "Guess" contains start values, which are the current thermodynamic data resulting in the green curve. I can adjust the parameters quite easily by hand so that the experimental data are well matched. In this case each equation is not at 0 but at values of <1000 (in J/mol), which would be ok (values of G for each phase are on the order of 1e6).

Without /T flag FindRoots results in an error message "…not making Progress…", which is not surprising, because I don't expect that conditions are found, where everything is exactly 0 or very close. Setting the /T flag to 1000 results in a successful operation (after 10 evaluations) but the start values do not change (and W_YatRoot has values of 2000-6000 for each element). This I find surprising, because I wonder what FindRoots did in the 10 evaluations and why there is no improvement compared to the start values. Finally some questions:

- have I used the correct format to enable FindRoots to do the job correctly?
- does the /T flag set the tolerance for each element or for something like the sum of W_YatRoot? If one or the other, why is it ignored here?
- is there any possibility to set lower and upper limits to the variables in this format. This might be part of the problem, because the equilibrium curve is very sensitive to some parameters
- ideally, if this runs stable I'd like to optimize data for more than one phase which could result in a set of 40-50 equations - I wonder if this would be the right strategy….

Thanks for reading all this
Christian
My first thought off the top of my head WRT strategy ...

You have all parameters to determine G_phase1 at any (T, p) conditions. So, generate G_phase1(T, p) first. Then, fit G_phase2(w, T, p) to the data points for G_phase1(T,p) using a fitting function approach rather than a FindRoots approach.

I would also be curious about your Gibbs(...) function needing a FindRoots numeric method to return a solution. Why might that be?

--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAHuntsville

July 5, 2011 at 12:23 pm - Permalink

jjweimer wrote:

You have all parameters to determine G_phase1 at any (T, p) conditions. So, generate G_phase1(T, p) first. Then, fit G_phase2(w, T, p) to the data points for G_phase1(T,p) using a fitting function approach rather than a FindRoots approach.


hm, the downside here is, and I simplified my task a bit in the above example, that I rather want to optimize the thermodynamic properties of both phases simultaneously. Each phase has parameters which are quite well constrained, others are not. So I might end up having 5 parameters of phase 2 and 3 parameters of phase 1 in the FindRoots system. This is why I really would like to set limits, because each parameter can only vary to a certain extent. And within this range I'd like to find an optimal solution.

jjweimer wrote:

I would also be curious about your Gibbs(...) function needing a FindRoots numeric method to return a solution. Why might that be?


I need the volume V of the phase at P and T which is calculated from a 3rd oder Birch-Murnaghan equation of state:

http://en.wikipedia.org/wiki/Birch–Murnaghan_equation_of_state

This is what needs a numerical solution.

July 5, 2011 at 02:11 pm - Permalink

Oh! You have an EoS for p = f(V, T) and measured data for p, T. Now you want to optimize the parameters in the EoS to best fit your measured (p, T) data at a phase boundary AND minimize a calculated Delta{}G(p, T) which itself is a function of the EoS(V, T) for each of the different phases. That is a classic higher order, grad-level pchem thermo problem!

I am confused by the need to use a minimization criteria on Delta{}G = G(2) - G(1) as a way to optimize parameters in the EoS which itself is correspondingly to be optimized against the measured data. It seems to be a rather convoluted way to do this from a principled stand, though I could be misunderstanding. Why not just obtain the best regression fit of the EoS for both phases to the measured (p,T) data as a way to obtain the best parameters for the EoS, and then calculate the Delta{}G (without optimization) afterward? You will have a far cleaner approach and can do a principled analysis of the propagation of uncertainties after fitting to find the confidence level in your Delta{}G truly being zero.

--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAHuntsville

July 5, 2011 at 03:46 pm - Permalink

jjweimer wrote:
Oh! You have an EoS for p = f(V, T) and measured data for p, T. Now you want to optimize the parameters in the EoS to best fit your measured (p, T) data at a phase boundary AND minimize a calculated Delta{}G(p, T) which itself is a function of the EoS(V, T) for each of the different phases.


well, the only thing I know for sure is that deltaG is zero at the phase boundary but I don't know the exact values of G. The experimental data in the plot do not deliver any physical properties directly - they only define where the phase boundary is. If I had measured e.g. volume as a function of T and P, I could fit the Birch-Murnaghan EOS parameters (this is essentially where the literature start values come from). I rather want to refine those values within their uncertainties to match the boundary. However, if you consider G as a surface in T-P space for a single phase it is continuous over T,P coordinates where phase boundary occur; it's only an intersecting G surface which shows where the transition is (see attached figure). Only if I knew the exact G values at the boundary I could fit one phase separately. Because I don't, I need deltaG = 0 as constraint.

Cheers
Christian
3D.png (60.65 KB)

July 6, 2011 at 03:02 am - Permalink

I understand the aspect of Delta{}G = 0 at the phase boundary. However, you also have an EoS for each phase. Should it not be a first principles requirement that your EoS for each phase fit the given (p, T) data? In such a case, it seems to me, the first principles approach should be to establish a proper method to fit the EoS for each phase to the given (p, T) data at the phase boundary, not "hide" that requirement in a higher level request to have Delta{}G = 0 at the phase boundary.

In other words, based on your phase diagram, the two phases have the same (p, T) at the phase boundary. That is true over the entire phase boundary. Make that a first order requirement to define the optimized parameters for the EoS for each phase. Set up a method to obtain the parameters that will recreate the entire (p, T) phase boundary data for each phase. Now, for each phase, you have the optimized parameters for its EoS. Use those parameters and the EoS to calculate the G values for each phase. Apply proper uncertainty analysis to determine the "error" in G (deltaG) based on the uncertainties in your parameters in the EoS. Calculate Delta{}G and its uncertainty (delta-Delta{}G). How confident then are you that Delta{}G is zero given the uncertainties delta-Delta{}G? That would be my approach.

Consider for liquid-gas systems that, when determining the a and b parameters in the van der Waals EoS, folks fit that EoS to the critical T, p data. They do NOT try to find the a and b parameters through a fit to a Delta{}G = 0 criteria at the critical point. Why should your approach to determine the parameters for your EoS be any different? Why should it require a higher level demand that Delta{}G = 0 as the way to obtain the parameters for the EoS?

--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAHuntsville

July 6, 2011 at 06:16 am - Permalink

As a follow-up ...

To focus this back to the use of Igor Pro, here is what I see. You have experimental data p versus T. You have a theoretical equation for p as a function of V(T), where V is a function of T. That equation also has parameters A(T), B(T), C, D, and E, where the first two are functions of T and the other two are constants.

I _think_ your approach in Igor Pro should be to develop a routine that will fit your p versus T data taking in to account V(T), A(T), B(T), C, D, and E. That routine will NOT include FindRoots (which I suspect you are applying at each p, T point), rather, it will do a global optimization on all of the p, T data to obtain the "best fit" parameters V(T), A(T), B(T), C, D and E.

Those folks who are more versed than me about the variety of ways to to optimal fitting of such multi-dimension data sets within Igor Pro should please chime in here.

After you have done this, you should use your equations for p to calculate the two G(p, T) values and Delta{}G(p, T) as well as the confidence limit in Delta{}G. I suspect you will find the uncertainty on Delta{}G = 0 will be below an otherwise reasonable +/- 10%, just based on the report you've given about the offset in the p(T) curve from the data. That will be well within what can be supported by the spread in your experimental data and in any case well below what you might otherwise expect from a "point-by-point" FindRoots approach embedded within a larger FindRoots routine.

--
J. J. Weimer
Chemistry / Chemical & Materials Engineering, UAHuntsville

July 6, 2011 at 09:43 am - Permalink