FFT Phase unwrapping

Share icon

Hello,
So I am working with a system that has a phase which isn't confined to [-pi,pi] and am running into a terrible time reproducing the phase after an FFT. For simplicity I have made a model to demonstrate the problem.

I start with a real valued Guassian wave Io.

I then define a complex wave I1=Io*exp(i*k)

with k being complex and defined as k=k'+i*k'', plugging in k I get:

I1=Io*e^(-k'')[Cos(k')+i*Sin(k)]

I then used an IFFT to give me IFT(I1). From there I took the FFT to get I1 back, or FT(IFT(I1))=I1.

I then found the phase and the magnitude,

taking -ln[FT(IFT(I1))/Io] I reproduced k'', but taking the phase and doing

unwrap pi,phase

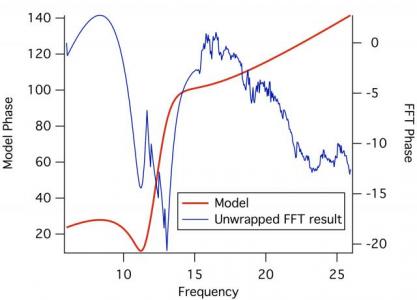
I got something that looks nothing like the model I used.

Comparing I1 and FT(IFT(I1)) I found that they have the same values for real and imaginary part, so I believe the issue is in the unwrapping procedure. Any ideas?


I have attached the project file and two graphs to show what I mean 2levelAbs.jpg (802.23 KB) 11162level.pxp (80.71 KB)