Stochastic ODE: Euler-Maruyama illustrated

 Stochastic ordinary differential equations have their own issues and require numerical methods that differ from those used for deterministic ODEs. While Igor does not support stochastic ODEs in an operation, it is straightforward to code explicitly the (simple) Euler-Maruyama (EM) method. In learning how to deal with such equations, I made the following code, which simulates a particle in a double-well potential of adjustable depth. It could be the starting point for explorations of stochastic resonance, information processing by small systems, etc. For this particular case, the EM method works well. For other applications, other algorithms such as Milstein's or Heun's methods may give better results. Note that the program uses 2 implicit loops, one to loop over the N time steps of an individual path, the other to calculate M paths.

If others are interested in stochastic methods, I encourage you to post more examples. This will perhaps persuade the Igor folks to add explicit support for stochastic equations. (While these methods are easy to program in Igor as it stands, they are much slower than what a C-coded version could do. And these calculations tend to require LOTS of iterations.....)

Note that this was developed in 6.10b07, but I see no reason that it won't run in Igor 6.0x.

//________________________________________________________________
 
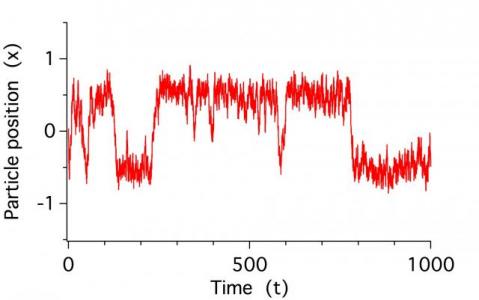
function em(M,N,D,Tf)                           // vector implementation of Euler-Maruyama
    variable M,N,D,Tf                       // M = paths, N = time points
                                    // D = noise strength, Tf = final sim. time
                                    // try M=1, N=1e4, D=0.01, Tf=1000
//  SetRandomSeed 0.5                       // useful for debugging
    variable dt = Tf/N, Xzero = 0                   // dt = time step;  Xzero = initial condition
    wave pars                           // declare parameter wave
    make /o/n=(M,N) dW
    dW = sqrt(2*D*dt)*gnoise(1)                 // M realizations of noise terms dW(t)
    Integrate /meth=2 /dim=1 dW /D=W                // integral is just sum of dW's
    Duplicate /o W, Xem
    Xem[][0] = Xzero                        // initialize all paths
    Xem[][1,N] =  Xem[p][q-1] + dt*myfunc(pars, (q-1)*dt, Xem[p][q-1]) + dW[p][q-1] 
                                    // this is the crucial step for the EM method!
    MatrixOp /o Xem0 = row(Xem,0)^t                 // get a single trajectory to graph     
    SetScale/P x 0,dt,"", Xem0
    killwaves dW,W,Xem                      // get rid of big waves
end
 
//________________________________________________________________
 
Function myfunc(pw,t,x)
    wave pw; variable t,x
                                    // t for time-dependent forces; not needed here
    variable a=pw[0]                        // barrier height  (try a=0.3)
    return a*x - x^3                        // force = -dU/dx, U = -a*x^2/2 + x^4/4
End
 
//________________________________________________________________
 
Window path_graphs() : Graph
    PauseUpdate; Silent 1       // building window...
    Display /W=(533,50,1004,389) Xem0
    ModifyGraph width=360,height=216
    ModifyGraph marker=19
    ModifyGraph msize=1
    ModifyGraph nticks(bottom)=2
    ModifyGraph fSize=18
    ModifyGraph manTick(left)={0,1,0,0},manMinor(left)={1,0}
    ModifyGraph manTick(bottom)={0,500,0,0},manMinor(bottom)={4,0}
    Label left "Particle position  (x)"
    Label bottom "Time  (t)"
    SetAxis left -1.5,1.5
    ControlBar 42
    SetVariable setvar0,pos={67,8},size={214,27},title="barrier height a  ",fSize=18
    SetVariable setvar0,limits={0,1,0.1},value= pars[0]
EndMacro

Forum

Support

Gallery

Igor Pro 9

Learn More

Igor XOP Toolkit

Learn More

Igor NIDAQ Tools MX

Learn More