Poisson Arrival Times

 Two years ago I submitted an Exchange response that approximated a wave of Poisson arrival times for generating a Data Acquisition output. Here is a more rigorous and general method, relying on the fact that inter-arrival times are exponentially distributed. The output wave contents are the sequential, cumulative times. By convention (?) the sequence starts with an event at t=0. In verifying Poisson statistics for the count numbers, the first point shoud be omitted. This function could be useful for Data Acquisition stimulus generation, or Igor simulations of classical shot-noise systems or queuing processes.
Function/WAVE fPoissonArrival(interval, lambda)  //  cumulative Poisson Arrival times in "wArrTime"
    variable interval, lambda  //  interval = counting interval; lambda = arrival rate/unit time
   
    make/O/N=1 wArrTime  //  this will contain the cumulative arrival times
    wArrTime[0] = 0
    variable i = 0
    Do
         i+=1
         InsertPoints  i+1, 1, wArrTime
         wArrTime[i] = wArrTime[i-1] + expnoise(1/lambda)  //  independent arrival increments are exponentially distributed
    While( wArrTime[i] < interval )  //  stop after interval exceeded
    DeletePoints  i, 1, wArrTime  //  delete last point, which is outside interval
    wave wout = wArrTime
    Return   wout  
End

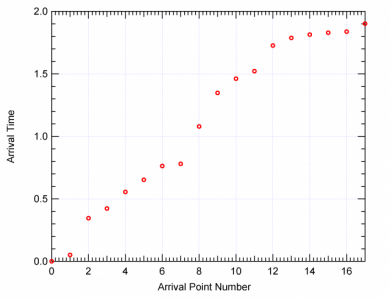
Attached is a graph of a typical output; Tests of repeated trials showed excellent agreement with the exact Poisson count distribution.
With recent improvements to Igor, this function returns a WAVE reference to the output. In your user function, it is used as:
WAVE wout = fPoissonArrival(interval, lambda)

I chose to use a simple, if inefficient, method for adding sequential arrival times. Using a pre-sized Igor wave might sometimes be quicker, but would ultimately require end-point checking, and either truncation or point addition since the 'a priori' number of arrivals is unknown.
Quote:
Thanks for sharing. Can this be used for Poisson Noise Waveform?

You are welcome. The intent of the snippet is indeed to enable the creation of a Poisson noise waveform. Use the arrival times in the returned wave to create your own impulse functions at those times, or by convolution with those impulses, any other pulse waveform of your choice. An "impulse" here means a single 'y' value in a wave at your closest scaled x-value (time) or vs the x-wave of arrival times.

January 6, 2013 at 02:47 pm - Permalink

Forum

Support

Gallery

Igor Pro 9

Learn More

Igor XOP Toolkit

Learn More

Igor NIDAQ Tools MX

Learn More