
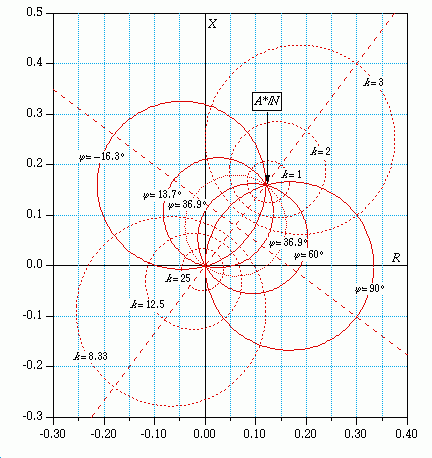
This graph is a plot of parametric variations, all of which happen to be circles. The basic equation is:
Z = R +jX = (c+ jd)/(1-ke^y)
where Z is a complex number in the R-X plane,the numerator is also a complex number, as noted, and the parameter y is psi. If we vary the parameter k, we get circles with centers that lie along the line A-B and if we vary the parameter y, we get circles with centers that lie along the perpendicular bisector and pass through points A and B. The circles are orthogonal and you will note that every crossing is at 90 degrees.
Submitted by Paul Anderson, Power Math Associates

Forum

Support
Gallery
Igor Pro 9
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More





