
The Jarque-Bera demo experiment can be used to generate the null distribution of the Jarque-Bera statistic for any number of variables (N). The Jarque-Bera statistic has asymptotically the Chi-square distribution with two degrees of freedom, i.e., StatsChiCDF(x,2). For small value of N the actual distribution is sufficiently different from the asymptotic values.
The calculation consists of a Monte-Carlo simulation which computes the Jarque-Bera statistic for many realizations of N random samples from a normal distribution. The wave containing the statistic is histogramed (using the /P flag it is also normalized as a PDF) and then integrated to get the corresponding CDF.
To obtain the critical value you can solve for the point at which the CDF equals 1-alpha, where alpha is the desired significance.
To run the simulation execute the following command.
WM_Jarque_BeraDistribution(1e6,22)
This will run 1 million iterations for N=22. The resulting CDF is stored in the wave W_JBCDF shown below.
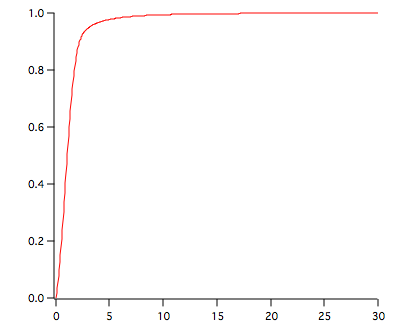
To find the critical value for alpha=0.05 execute the command:
FindLevel W_JBCDF, 0.95
The results are: V_LevelX= 3.09913; V_rising= 1;
By comparison, the asymptotic approximation is give by:
Print StatsInvChiCDF(0.95,2)
which yields 5.99146.
This indicates that for N=22 there is a significant difference between the asymptotic approximation and the critical value obtained from this calculation.
More Details
The simulation uses WaveStats to compute skewness and kurtosis. WaveStats uses a two-pass algorithm to compute the higher order moments (i.e., the first pass computes the average value and the second pass computes the various central moments). The two-pass algorithm is supposed to provide higher accuracy (see, for example, a discussion in Numerical Recipes) then algorithms that evaluate the binomial expansion sums of wave elements. Here is an example of the difference between the two methods of computation:
Make/O/N=1e5 ddd=gnoise(10) KurtosisComparison(ddd)
Kurtosis(WaveStats)=-0.013552
Kurtosis(binomial expansion sums)=-0.0134328

Forum

Support

Gallery
Igor Pro 10
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More