
The following functions return numbers from pseudo-random distributions of the specified shapes and parameters. Except for enoise and gnoise where you have an option to select a random number generator, the remaining noise functions use a Mersenne Twister algorithm for the initial uniform pseudo-random distribution. Note that whenever you need repeatable results you should use SetRandomSeed prior to executing any of the noise functions.
Built-in noise functions and distributions
| Noise Function | Distribution |
| binomialNoise | Binomial distribution |
| enoise | Uniform distribution |
| expNoise | Exponential distribution |
| gammaNoise | Gamma distribution |
| gnoise | Gaussian distribution |
| HyperGNoise | Hypergeometric distribution |
| logNormalNoise | Lognormal distribution |
| poissonNoise | Poisson distribution |
| StatsPowerNoise | Power distribution |
| StatsVonMisesNoise | Von Mises distribution |
| WNoise | Two-parameter Weibull distribution |
You can easily verify that the various noise functions indeed generate the desired distribution. For example, suppose you generated 10000 data points from a Gamma distribution as in:
Make/O/N=1e4 noiseWave=gammaNoise(10,2)
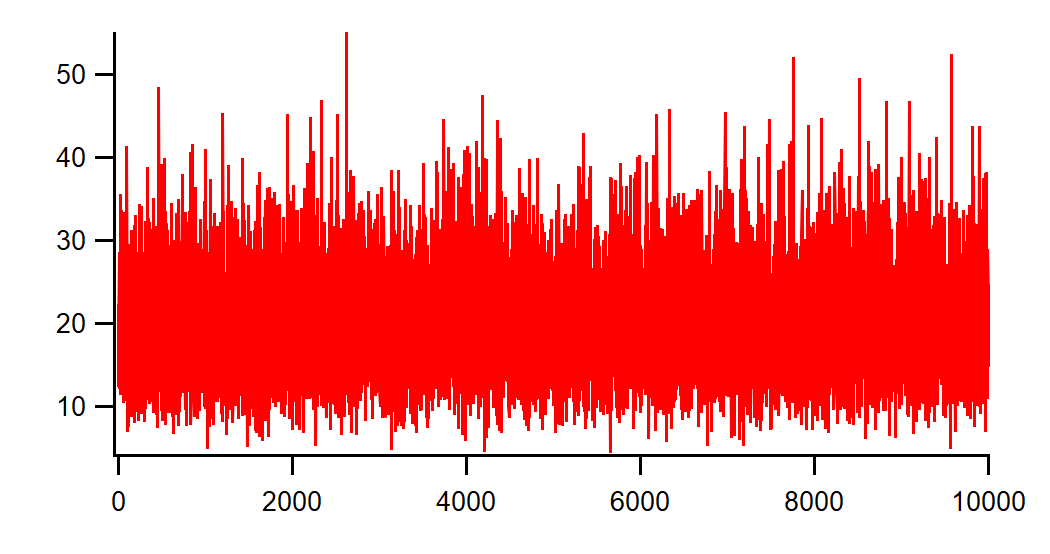
Make/O/N=100/O W_Hist Histogram/P/B={0,1,100} noiseWave,W_Hist
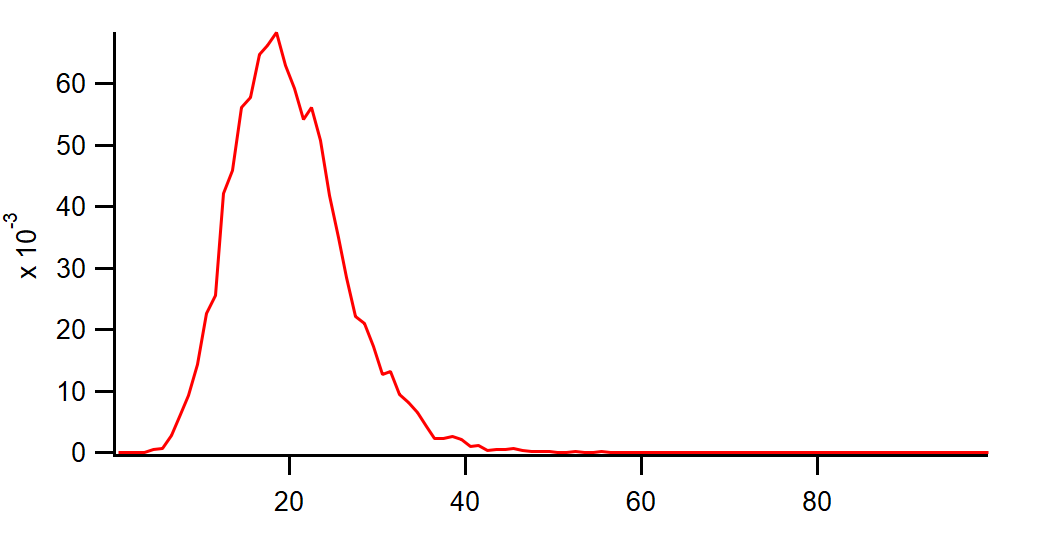
To fit this to a gamma distribution we write the following user function:
Function myFit(w,x) : FitFunc Wave w Variable x return x^(w[0]-1)*exp(-x/w[1])/((w[1]^w[0])*Gamma(w[0])) End
To determine the initial guesses for the fitting coefficients we note that the average of noiseWave is 19.8681. This average should be equal to the product a*b of the two parameters of the gamma distribution. Our guess is therefore a=b=sqrt(19.8)
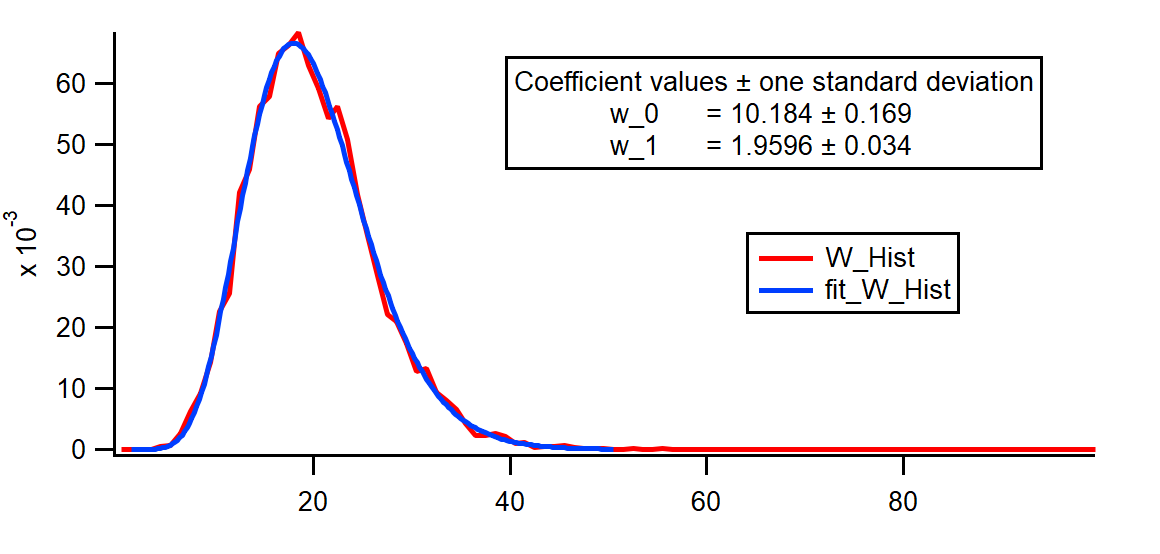
Make/O/D/N=2 W_coef={4.48,4.48} FuncFit/NTHR=0/TBOX=768 myFit W_coef W_Hist[1,50] /D
The resulting fit to a Gamma distribution is drawn below in blue plotted over the calculated distribution (red).

Forum

Support
Gallery
Igor Pro 10
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More