
Smoothing removes short-term variations, or "noise" to reveal the important underlying unadulterated form of the data.
Igor Pro®´s Smooth operation performs box, "binomial", and Savitzky-Golay smoothing. The different smoothing algorithms convolve the input data with different coefficients.
Smoothing is a kind of low-pass filter. The type of smoothing and the amount of smoothing alters the filter´s frequency response:
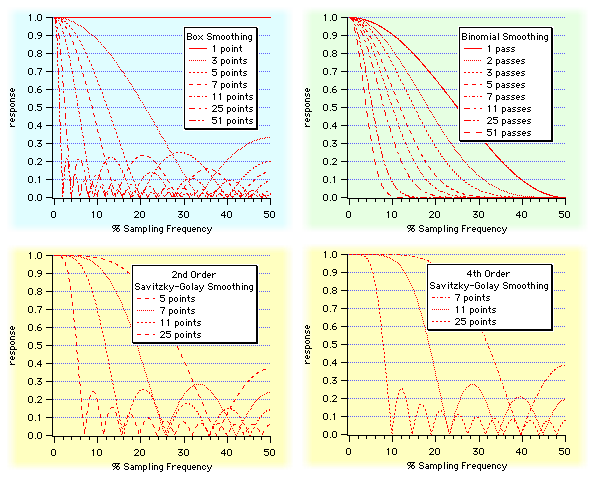
Moving Average (aka "Box Smoothing")
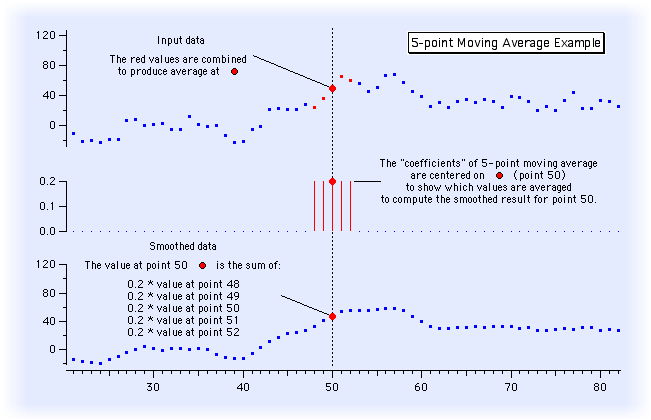
The simplest form of smoothing is the "moving average" which simply replaces each data value with the average of neighboring values. To avoid shifting the data, it is best to average the same number of values before and after where the average is being calculated. In equation form, the moving average is calculated by: ![x hat[i] = 1/(2*M+1) * sum from -M to +M of x[i+j]](/sites/www.wavemetrics.com/files/images-imported/movingaverageeqn_3.png)
Another term for this kind of smoothing is "sliding average", "box smoothing", or "boxcar smoothing". It can be implemented by convolving the input data with a box-shaped pulse of 2*M+1 values all equal to 1/(2*M+1). We call these values the "coefficients" of the "smoothing kernel":
Binomial Smoothing
Binomial smoothing is a Gaussian filter. It convolves your data with normalized coefficients derived from Pascal´s triangle at a level equal to the Smoothing parameter. The algorithm is derived from an article by Marchand and Marmet (1983).
Savitzky-Golay Smoothing
Savitzky-Golay smoothing uses a different set of precomputed coefficients popular in the field of chemistry. It is a type of Least Squares Polynomial smoothing. The amount of smoothing is controlled by two parameters: the polynomial order and the number of points used to compute each smoothed output value.
References
- Marchand, P., and L. Marmet, Binomial smoothing filter: A way to avoid some pitfalls of least square polynomial smoothing, Rev. Sci. Instrum., 54, 1034-41, 1983.
- Savitzky, A., and M.J.E. Golay, Smoothing and differentiation of data by simplified least squares procedures, Analytical Chemistry, 36, 1627-1639, 1964.

Forum

Support

Gallery
Igor Pro 10
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More