• The Fourier transform has long been used for characterizing linear systems and for identifying the frequency components making up a continuous waveform. However, when the waveform is sampled, or the system is to be analyzed on a digital computer, it is the finite, discrete version of the Fourier transform (DFT) that must be understood and used. Although most of the properties of the continuous Fourier transform (CFT) are retained, several differences result from the constraint that the DFT must operate on sampled waveforms defined over finite intervals.


• The fast Fourier transform (FFT) is simply an efficient method for computing the DFT... [1];

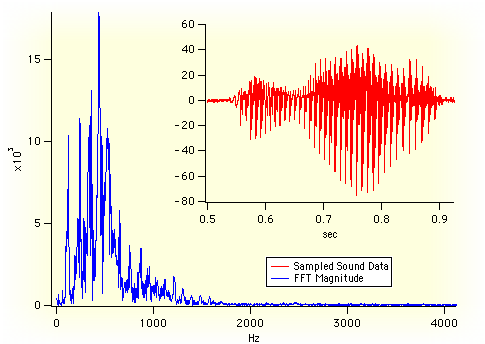
The Fourier Transform’s ability to represent time-domain data in the frequency domain and vice-versa has many applications. One of the most frequent applications is analysing the spectral (frequency) energy contained in data that has been sampled at evenly-spaced time intervals. Other applications include fast computation of convolution (linear systems responses, digital filtering, correlation (time-delay estimation, similarity measurements) and time-frequency analysis.

The fast version of this transform, the Fast Fourier Transform (or FFT) was first developed by Cooley and Tukey [2] and later refined for even greater speed and for use with different data lengths through the “mixed-radix” algorithm. Igor Pro® computes the FFT using a fast multidimensional prime factor decomposition Cooley-Tukey algorithm.

While the the Fourier Transform is mathematically complicated, Igor’s Fourier Transforms dialog makes it easy to use:

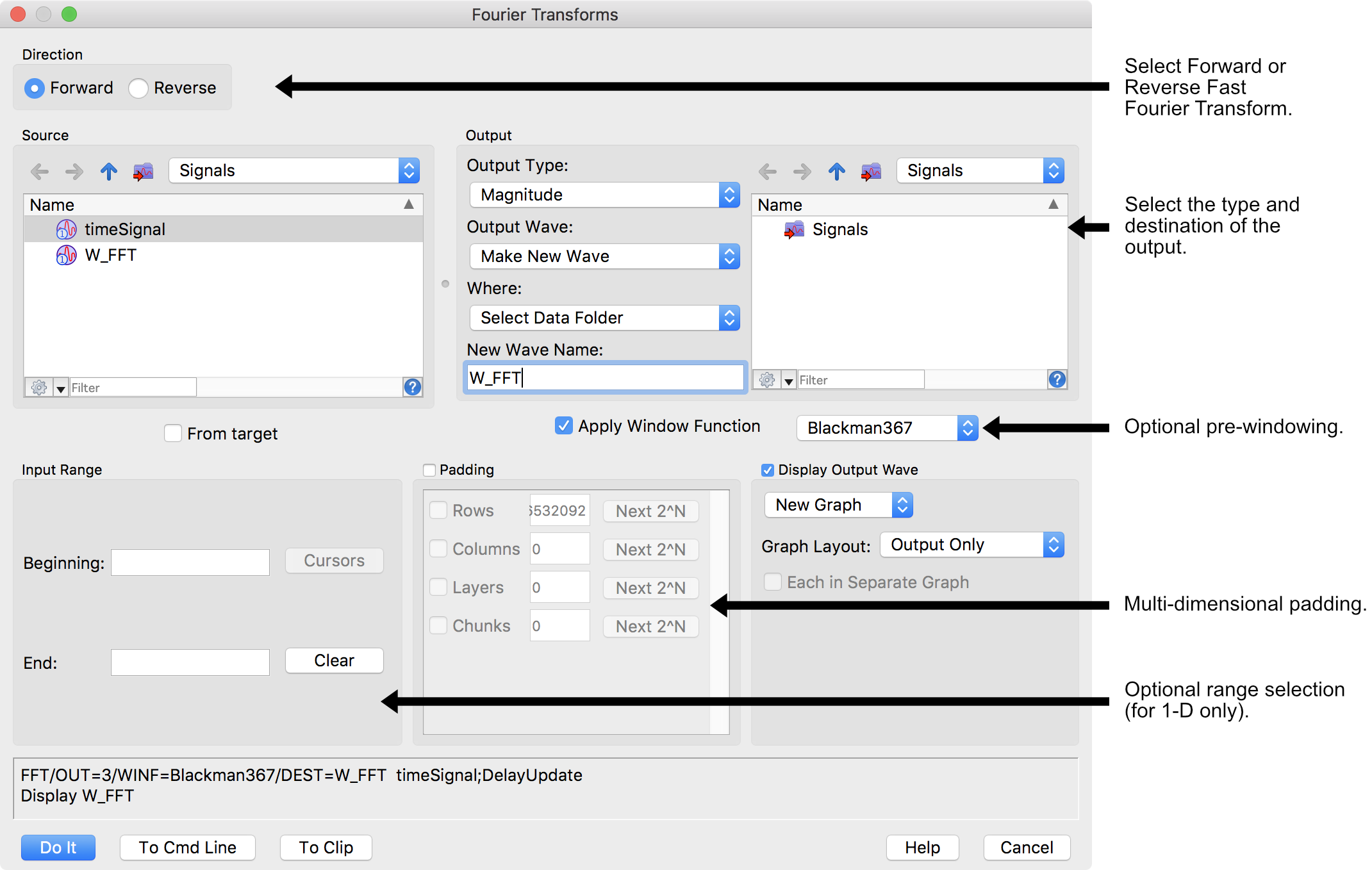
Igor’s FFT operation supports advanced calculations, some of which are beyond the scope of the Fourier Transforms dialog:

• FFT of 2-Dimensional, 3-D, and 4-D data
• Input Data Length Padding
• Input Data Windowing
• Results as Complex, Real-only, Imaginary-only, Magnitude, Magnitude Squared, or Phase
• Hypercomplex sine transform < li >Hypercomplex cosine transform

In addition to the FFT, Igor provides these other transforms:

• Periodogram
• Lomb Periodogram
• MultiTaperPSD
• Discrete Wavelet Transform (DWT)
• Continuous Wavelet Transform (CWT)
• Wigner Transform
• Short-Time Fourier Transform Transform
• Hilbert Transform

References

1. G.D. Bergland, “A guided tour of the fast Fourier transform,” IEEE Spectrum 7, 41-52 (1969).
2. James W. Cooley and John W. Tukey, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19, 297-301 (1965).